Giải bài 38 tr 91 sách GK Toán lớp 6 Tập 2
Trong hình 48, ta có hai đường tròn(O;2cm) và (A;2cm) cắt nhau tại C,D. Điểm A nằm trên đường tròn tâm O.
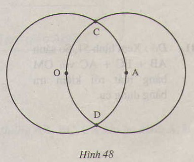
a) Vẽ đường tròn tâm C, bán kính 2cm.
b) Vì sao đường tròn(C;2cm) đi qua O,A?
Hướng dẫn giải chi tiết
Câu a:
Xem hình bên
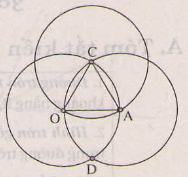
Câu b:
Đường tròn (C;2cm) đi qua O và A vì O và A cách C là 2cm.
-- Mod Toán 6 HỌC247
-


Trên hình sau đây, ta có hai đường tròn (A; 3cm) và (B; 2cm) cắt nhau tại C, D, AB = 4cm . Đường tròn tâm A, B lần lượt cắt đoạn thẳng AB tại K, I.
bởi Bo Bo
 19/01/2021
19/01/2021
a) Tính CA, CB, DA, DB.
b) I có phải là trung điểm của đoạn thẳng AB không?
c) Tính IK.
.png) Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


Cho hình vẽ dưới đây, ta có hai đường tròn (O; 2cm) và (A; 2cm) cắt nhau tại C,D. Điểm A nằm trên đường tròn tâm O.
bởi thu hằng
 19/01/2021
19/01/2021
Cho hình vẽ dưới đây, ta có hai đường tròn (O; 2cm) và (A; 2cm) cắt nhau tại C,D. Điểm A nằm trên đường tròn tâm O.
a) Vẽ đường tròn tâm C, bán kính 2cm.
b) Vì sao đường tròn (C; 2cm) đi qua O, A?
.png) Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


Cho hai điểm A, B cách nhau một khoảng bằng 4cm. Tìm điểm M có khoảng cách đến A một đoạn 3cm và có khoảng cách đến B một đoạn 2cm. Có bao nhiêu điểm như vậy?
bởi Aser Aser
 20/01/2021
Theo dõi (0) 1 Trả lời
20/01/2021
Theo dõi (0) 1 Trả lời -


Cho hai điểm A, B cách nhau một khoảng bằng 4cm. Các điểm cách A một khoảng 3cm nằm trên đường nào? Cách điểm B một khoảng 2cm nằm trên đường nào?
bởi Huong Giang
 19/01/2021
Theo dõi (0) 1 Trả lời
19/01/2021
Theo dõi (0) 1 Trả lời -


Cho đường thẳng a và điểm A ∈ a , một độ dài R = 4cm. Trên đường thẳng a có bao nhiêu điểm cách điểm A một đoạn 4cm. Xác định các điểm ấy
bởi thu hảo
 20/01/2021
Theo dõi (0) 1 Trả lời
20/01/2021
Theo dõi (0) 1 Trả lời -


Cho đường thẳng a và điểm A ∈ a , một độ dài R = 4cm. Các điểm M trong mặt phẳng có khoảng cách đến điểm A bằng 4cm thì nằm trên đường nào
bởi Nguyễn Quang Minh Tú
 19/01/2021
Theo dõi (0) 1 Trả lời
19/01/2021
Theo dõi (0) 1 Trả lời -


Cho hình vẽ sau, có bao nhiêu bán kính ở trong hình?
bởi Lan Anh
 13/01/2021
13/01/2021
.png)
A. 1
B. 2
C. 3
D. 4
Theo dõi (0) 1 Trả lời -


.png)
A. 0
B. 1
C. 2
D. 3
Theo dõi (0) 1 Trả lời -


Chọn phát biểu sai trong các phát biểu sau:
bởi Bao Chau
 14/01/2021
14/01/2021
A. Hình gồm các điểm nằm trên đường tròn và các điểm nằm trong đường tròn đó là hình tròn.
B. Dây cung không đi qua tâm là bán kính của đường tròn đó.
C. Hai điểm A và B của một đường tròn chia đường tròn đó thành hai cung. Đoạn thẳng nối hai mút của một cung là dây.
D. Dây cung đi qua tâm là đường kính của đường tròn đó.
Theo dõi (0) 1 Trả lời -


Chọn phát biểu đúng trong các phát biểu sau:
bởi Lê Chí Thiện
 14/01/2021
14/01/2021
A. Đường tròn tâm O, bán kính R là hình gồm các điểm cách O một khoảng bằng R, kí hiệu là (O; R).
B. Đường tròn tâm O, đường kính R là hình gồm các điểm cách O một khoảng bằng R, kí hiệu là (O; R).
C. Đường tròn tâm O, bán kính R là hình gồm các điểm cách O một khoảng bằng R/2, kí hiệu là (O; R).
D. Hình tròn tâm O, bán kính R là hình gồm các điểm cách O một khoảng bằng R, kí hiệu là (O; R).
Theo dõi (0) 1 Trả lời -


Đường tròn tâm N có vị trí như thế nào?
bởi Nguyễn Thị Phương
 19/07/2020
19/07/2020
 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Điểm A nằm trong (O;5cm) thì OA có bằng 5cm không?
bởi Chuong Le
 24/06/2020
24/06/2020
 Theo dõi (0) 3 Trả lời
Theo dõi (0) 3 Trả lời -


Tính CA, CB, DA, DB?
bởi Thang Hồng Ngọc
 12/06/2020
12/06/2020
 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời
Bài tập SGK khác
Bài tập 39 trang 92 SGK Toán 6 Tập 2
Bài tập 40 trang 92 SGK Toán 6 Tập 2
Bài tập 41 trang 92 SGK Toán 6 Tập 2
Bài tập 42 trang 93 SGK Toán 6 Tập 2
Bài tập 35 trang 93SBT Toán 6 Tập 2
Bài tập 36 trang 93 SBT Toán 6 Tập 2
Bài tập 37 trang 93 SBT Toán 6 Tập 2
Bài tập 38 trang 93 SBT Toán 6 Tập 2
Bài tập 39 trang 93 SBT Toán 6 Tập 2
Bài tập 8.1 trang 94 SBT Toán 6 Tập 2





