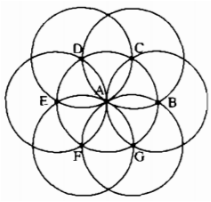
Bài tập 8.1 trang 94 SBT Toán 6 Tập 2

1)cho hpt:\(\left\{{}\begin{matrix}x+y=3\\2x-my=1\end{matrix}\right.\)

a)giải khi m=-7

b)tìm m để hpt có no(-1,4)

c)tìm m để hpt có no duy nhất

d)tìm m để hpt có no(x,y) với x,y thuộc z

Cho tứ giác ABCD nội tiếp (O; R). Gọi I là giao điểm AC và BD. Kẻ IH vuông góc với AB; IK vuông góc với AD \(\left(H\in AB;K\in AD\right)\).

a/ CM tứ giác AHIK nội tiếp

b/ CM: IA.IC=IB.ID

c/ CMR: tam giác HIK và tam giác BCD đồng dạng

d/ Gọi S là diện tích tam giác ABD, S' là diện tích tam giác HIK. CMR: \(\dfrac{S'}{S}\le\dfrac{HK^2}{4AI^2}\)

định nghĩa bán kính

Cho điểm A cố định nằm ngoài đường tròn (O;R). Tìm tập hợp các trung điểm M của đoạn thẳng AB khi B di động trên (O;R)

Cho đường tròn (O) đường kính AB. Vẽ đường tròn (I) đường kính OA. Bán kính OC của đường tròn (O) cắt đường tròn (I) tại D. Vẽ CH ⊥ AB. CM tứ giác ACDH là hình thang cân.

Cho hình thoi ABCD. Gọi O là giao điểm hai đường chéo: M, N, R và S lần lượt là hình chiếu của O trên AB, BC, CD và DA. CM 4 điểm M, N, R, S cùng thuộc một đường tròn.

Cho đường tròn ( O ;R ). Từ điểm M ngoài đường tròn , kể 2 tiếp tuyến MA , MB ( A , B là 2 tiếp điểm ) . Lấy điểm C bất kì trên cung nhỏ AB ( C khác A,B ) . Gọi D , E , F lần lượt là hình chiếu vuông góc của C trên AB , AM , BM .

a/ CM tứ giác AECD nội tiếp đường tròn .

b/ CMR góc CDE = góc CBA .

c/ Gọi I là giao điểm của AC và ED , K là giao điểm của CD và DF . Chứng minh : IK // AB .

a , cho a,b là 2 số thực dương tùy ý . Cmr \(\dfrac{a}{b}+\dfrac{b}{a}\ge2\)

b. Cho 3 số thực dương x,y,z thỏa mãn : x+y+z=1

Tìm giá trị lón nhất của biểu thức : P=\(\dfrac{x}{x+1}+\dfrac{y}{y+1}+\dfrac{z}{z+1}\)

Trên đường tròn (O; R) lấy 10 điểm phân biệt:

a. Hỏi qua 10 điểm đó vẽ được bao nhiêu dây? Bao nhiêu cung?

b. Trên hình vẽ có tất cả bao nhiêu góc.

c. Cũng hỏi như trên với n điểm trên đường tròn.

Bài 1: Cho nửa ĐT(O), đường kính AB. Qua C thuộc nửa đường tròn kẻ tiếp tuyến d với đường tròn. Gọi E, F thứ tự là hình chiếu của AB trên d. Kẻ CH vuông góc với AB.Chứng minh rằng:

a) CE = CF

b) AC là phân giác của góc BAE

c) CH^2 = AE . BF

Cho tam giác ABC có 3 góc nhọn nội tiếp đường tròn tâm (O;R). Vẽ hai đường cao BD và CE của tam giác ABC cắt nhau tại H. DE cắt đường tròn (O) tại P và Q (P thuộc cung nhỏ AB).
a) C/m tứ giác BEDC nội tiếp, xác định tâm
b) C/m BH.DH = EH.HC
c) C/m tam giác APQ cân tại A và AP2 = AE.AB
d) Gọi S1 là diện tích tam giác APQ, S2 là diện tích tam giác ABC. Giả sử: \(\dfrac{S_1}{S_2}=\dfrac{PQ}{2BC}\). Tính BC theo R

Cho tam giác ABC vuông tại A, đường cao AH.Gọi D và E lần lượt là hình chiếu của điểm H trên các cạnh AB và AC. 1.Chứng minh AD.AB=AE.AC .

2.Gọi M,N lần lượt là trung điểm của BH và CH. Chứng minh DE là tiếp tuyến chung của hai đường tròn (M;MD) và (N;NE).

3. Gọi P là trung điểm của MN, Q là giao điểm của DE và AH. Gỉa sử AB=6cm, AC=8cm. Tính độ dài PQ.

Giúp mình với. Mai thầy kiểm tra bài này rồi. Mình ngu toán hình cực.

Cho đường tròn (O) có hai đường kính AB và CD vuông góc với nhau. Một đường thẳng a di động qua C, cắt AB tại M và tiếp tuyến của đường tròn (O) tại N. Đường thẳng vuông góc với AB tại M và tiếp tuyến của đường tròn (O) tại N cắt nhau tại P.

1/ Chứng minh rằng OP // a

2/ Tìm tập hợp những điểm P khi a dao động.

( Không cần hình vẽ đâu ạ, giúp em cái hướng và cách chứng minh ạ, em cảm ơn )