Bài tập 37 trang 93 SBT Toán 6 Tập 2
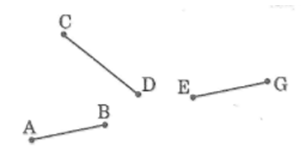
Làm thế nào để chỉ đo một lần, mà biết được tổng độ dài các đoạn thẳng ở hình bên .
Hướng dẫn giải chi tiết
Kẻ tia Oy. Dùng compa đặt các đoạn AB, CD, EG liên tiếp trên tia Oy sao cho điểm A trùng điểm O, điểm C trùng điểm B, điểm E trùng điểm D. Đo đoạn OG. Độ dài đoạn thẳng OG chính là độ dài ba đoạn thẳng trên
-- Mod Toán 6 HỌC247
-


Cho đường tròn (T) tâm O và đường kính AB cố định. Gọi M là điểm di động trên (T) sao cho M không trùng với các điểm A và B. Lấy C là điểm đối xứng của O qua A. Đường thẳng vuông góc với AB tại C cắt đường thẳng AM tại N. Đường thằng BN cắt đường tròn (T) tại điểm thứ hai là E. Các đường thẳng BM và CN cắt nhau tại F.
a, Chứng minh rằng các điểm A,E,F thẳng hàng.
b, Chứng minh rằng tích AM.AN không đổi.
c, Chứng minh rằng A là trọng tâm của tam giác BNF khi và chỉ khi NF ngắn nhất.
Theo dõi (0) 1 Trả lời -


Chứng minh tam giác MON vuông
bởi thanh hằng
 24/01/2019
24/01/2019
Câu 1: Cho nửa đường tròn (O:R), đường kính AB. Gọi Ax, By là các tia vuông góc với AB (Ax, By) và nửa đường tròn thuộc cùng 1 nữa mặt phẳng bờ là AB). Gọi M là điểm bất kì thuộc tia Ax. Qua M kẻ tiếp tuyến với nửa đường tròn, cắt by ở N.
a) CM tam giác MON vuông
b) CMR MN = AM + BN
c) CMR AM . BN = \(R^2\)
Câu 2: Cho đường trong (O), điểm A năm bên ngoài đường tròn. Kẻ các tiếp tuyến AM, AN vs đường tròn (M, N là các tiếp điểm).
a) CMR: OA vuông góc vs MN
b) Vẽ đường kính NC, cmr: MC//OA
c) Tính độ dài các cạnh của tam giác AMN, biết OA=5cm, ON= 3cm
Theo dõi (0) 1 Trả lời -


Chứng minh tứ giác MOHE nội tiếp
bởi Nguyễn Sơn Ca
 24/01/2019
24/01/2019
Cho đường tròn (O) đường kính AB, lấy điểm M bất kì trên đường tròn. Qua điểm H thuộc đoạn OB vẽ đường thẳng d vuông góc với AB, đường thẳng d cắt các đường thẳng MA, MB lần lượt tại D, C . Tiếp tuyến tại M của đường tròn cắt đường thẳng d tại I , tia AC cắt đường tròn tại E, đường thẳng ME cắt OI tại K. Chứng minh :
a, Tứ giắc MOHE nội tiếp
b, IE là tiếp tuyến của đường tròn (O)
c, Đường thẳng ME đi qua điểm cố định
Theo dõi (0) 1 Trả lời -


Chứng minh CD = AC + BD và tam giác COD vuông tại O
bởi Nguyễn Lê Tín
 24/01/2019
24/01/2019
Cho nửa đường tròn tâm O , đường kính AB = 2R . M là 1 điểm tùy ý trên đường tròn, M khác A, B. Kẻ 2 tiêp stuyeens Ax, By với nửa đường trong ( Ax, By và nửa đường trong cùng nằm trên một mặt phẳng bờ AB ) . Qua M kẻ tiếp tuyến thứ 3 với đường trong cắt Ax và By tại C và D .
a). Chứng minh : CD = AC + BD và tam giác COD vuông tại O
b). Chứng minh : AC.BD = R2
c). Cho biết AM = R . Tính theo R diện tích tam giác BDM
d). AD cắt BC tại N. Chứng minh MN song song ACTheo dõi (0) 1 Trả lời -


Chứng minh rằng tam giác BFE đồng dạng tam giác BDC
bởi hi hi
 24/01/2019
24/01/2019
Cho tam giác BCD có 3 góc nhọn. Các đường cao CE và DF cắt nhau tại H.
1. CM: tg BFHE nội tiếp
2. CMR: tam giác BFE đồng dạng tam giác BDC
3. Kẻ Ey : tiếp tuyến của (O; CD/2) cắt BH tại N
CMR: N là trung điểm BH
Giúp mình câu 3 thôi ạ. Hai câu trên mình làm được rồi. Thanks
Theo dõi (0) 1 Trả lời -


Chứng minh ABOC nội tiếp, biết OA cắt BC tại E
bởi Hong Van
 24/01/2019
24/01/2019
Cho đường tròn (O), từ điểm A ngoài đường tròn vẽ 2 tiếp tuyến AB và AC( B, C là tiếp điểm). OA cắt BC tại E
1)CM: ABOC nội tiếp
2)CM: BC vuông góc với OA và BA.BE=AE .BO
3) Gọi I là trung điểm BE, đường thẳng qua I và vuông góc với OI cắt AB, AC tại D và F. CM: IDO=BCO và tam giác DOF cân tại O
4)CM: F là trung điểm AC
Theo dõi (0) 1 Trả lời -


Tính diện tích phần mũi tên của biển báo giao thông hình tròn có bán kính 3dm
bởi Tran Chau
 02/11/2018
02/11/2018
Một biển báo giao thông là một hình tròn có bán kính 3dm và một mũi tên nằm trong hình tròn.Diện tích phần mũi tên trên biển báo bằng 1/9 diện tích hình tròn. Tính diện tích phần mũi tên
Theo dõi (0) 6 Trả lời -


Chứng minh tam giác BCE đều và OI _|_ DC
bởi Lan Ha
 25/01/2019
25/01/2019
Cho hình bình hành ABCD có tam giác ADC nhọn, ADC^ = 60o. Đường tròn tâm O ngoại tiếp tam giác ADC cắt cạnh AB tại E ( E khác A), AC cắt DE tại I.
a) Chứng minh tam giác BCE đều và OI _|_ DC
b) Gọi K là trung điểm BD, Ko cắt DC tại M. Chứng minh A,D,M,I cùng thuộc một đường tròn
c) Gọi J là tâm đường tròn ngoại tiếp tam giác ABC. Tính OJ/DE
b thôi (nếu thêm được c thì càng tốt) . Thanks a lot!
Theo dõi (0) 1 Trả lời -


Cho tam giác ABC vuông tại A, đường cao AH. Vẽ đường tròn tâm A, bán kính AH.
a) Chứng tỏ BC là tiếp tuyến của đường tròn tâm A bán kính AH
b) Từ B và C vẽ các tiếp tuyến BD, CE với đường tròn( D,E là các tiếp điểm). Chứng minh D,A,E thẳng hàng.
c) Gọi Mlaf giao điểm của AB và DH, N là giao điểm AC và EH. Chứng mnih MN//DE
d) Chứng minh HB.HC= AM.AB
Ai guips mik vs!!!!! thanks trước.
Theo dõi (0) 1 Trả lời -


Chứng minh các tứ giác ADHE, BCDE nội tiếp
bởi Tieu Dong
 25/01/2019
25/01/2019
cho tam giác nhọn ABC nội tiếp trong đường tròn tâm O . Đường ca BD và CE cắt nhau tại H
a) CM các tứ giác ADHE,BCDE nội tiếp
b) Tia BD và CE lần lượt cắt đường tròn (O) tại M và N cm DE//MN
Theo dõi (0) 1 Trả lời -


Chứng minh OA ⊥ BC
bởi het roi
 25/01/2019
25/01/2019
Cho đường tròn (O;R). Từ điểm A nằm ngoài đường trong vẽ hai tiếp tuyến AC và AB (B và C là các tiếp điểm)
a) Chứng minh OA \(\perp\) BC
b) Từ O vẽ OK// AB (K\(\in\) AC). Cm: OK=AK
c) Đường thẳng OB cắt (o) tại điểm thứ hai M và cát AC tại N. Chứng minh CM// OA
d) Cm: OM.AN = AC.ON
Theo dõi (0) 1 Trả lời -


Tính diện tích tam giác vuông
bởi Lê Tấn Thanh
 25/01/2019
25/01/2019
Tính diện tích tam giác vuông
Theo dõi (0) 1 Trả lời -


Chứng minh tứ giác ACMD nội tiếp
bởi Goc pho
 25/01/2019
25/01/2019
Cho nửa đường tròntâm O đường kính AB. Lấy điểm C trên đoạn thẳng AO ( C khác A và O ). đường thẳng đi qua C vuông góc với AB cắt nửa đường tròn tại K. Gọi M là giao điểm bất kì trên cung KB. Đường thẳng CK cắt đường thẳng AM, BM lần lượt tại H và D. Đường thẳng Bh cắt nửa đường tròn tại N
a) c/m tứ giác ACMD nội tiếp
b) C/m: CA.CB=CH.CD
c) c/m 3 điểm A,N,D thảng hàng và tiếp tuyến tại N thuộc nửa đường tròn đi qua trung điểm của DH
Theo dõi (0) 1 Trả lời
Bài tập SGK khác
Bài tập 38 trang 91 SGK Toán 6 Tập 2
Bài tập 39 trang 92 SGK Toán 6 Tập 2
Bài tập 40 trang 92 SGK Toán 6 Tập 2
Bài tập 41 trang 92 SGK Toán 6 Tập 2
Bài tập 42 trang 93 SGK Toán 6 Tập 2
Bài tập 35 trang 93SBT Toán 6 Tập 2
Bài tập 36 trang 93 SBT Toán 6 Tập 2
Bài tập 38 trang 93 SBT Toán 6 Tập 2
Bài tập 39 trang 93 SBT Toán 6 Tập 2
Bài tập 8.1 trang 94 SBT Toán 6 Tập 2