HŲ░ß╗øng dß║½n Giß║Żi b├Āi tß║Łp To├Īn 11 Kß║┐t nß╗æi tri thß╗®c ChŲ░ŲĪng 5 B├Āi 15 Giß╗øi hß║Īn cß╗¦a d├Ży sß╗æ m├┤n To├Īn hß╗Źc lß╗øp 11 gi├║p c├Īc em hß╗Źc sinh nß║»m vß╗»ng phŲ░ŲĪng ph├Īp giß║Żi b├Āi tß║Łp v├Ā ├┤n luyß╗ćn tß╗æt kiß║┐n thß╗®c.
-
Hoß║Īt ─æß╗Öng 1 trang 105 SGK To├Īn 11 K├¬╠üt n├┤╠üi tri thŲ░╠üc tß║Łp 1 - KNTT
Cho d├Ży sß╗æ (\({u_n}\)┬Ł) vß╗øi \({u_n} = \frac{{{{\left( { - 1} \right)}^n}}}{n}\).
a) Biß╗āu diß╗ģn n─ām sß╗æ hß║Īng ─æß║¦u cß╗¦a d├Ży sß╗æ n├Āy tr├¬n trß╗źc sß╗æ.
b) Bß║»t ─æß║¦u tß╗½ sß╗æ hß║Īng n├Āo cß╗¦a d├Ży, khoß║Żng c├Īch tß╗½ un ─æß║┐n 0 nhß╗Å hŲĪn 0,01?
-
Luyß╗ćn tß║Łp 1 trang 105 SGK To├Īn 11 K├¬╠üt n├┤╠üi tri thŲ░╠üc tß║Łp 1 - KNTT
Chß╗®ng minh rß║▒ng \(\mathop {\lim }\limits_{n \to + \infty } \frac{{{{\left( { - 1} \right)}^{n - 1}}}}{{{3^n}}} = 0\).
-
Hoß║Īt ─æß╗Öng 2 trang 105 SGK To├Īn 11 K├¬╠üt n├┤╠üi tri thŲ░╠üc tß║Łp 1 - KNTT
Cho d├Ży sß╗æ \(\left( {{u_n}} \right)\) vß╗øi \({u_n} = \frac{{n + {{\left( { - 1} \right)}^n}}}{n}\). X├®t d├Ży sß╗æ \(\left( {{v_n}} \right)\) x├Īc ─æß╗ŗnh bß╗¤i \({v_n} = {u_n} - 1\). T├Łnh \(\lim\limits_{n\to\infty}{v_n}\)┬Ł.
-
Luyß╗ćn tß║Łp 2 trang 106 SGK To├Īn 11 K├¬╠üt n├┤╠üi tri thŲ░╠üc tß║Łp 1 - KNTT
Cho d├Ży sß╗æ \(\left( {{u_n}} \right)\) vß╗øi \({u_n} = \frac{{{{3.2}^n} - 1}}{{{2^n}}}\). Chß╗®ng minh rß║▒ng \(\mathop {lim}\limits_{n \to + \infty } {u_n} = 3\).
-
Vß║Łn dß╗źng 1 trang 106 SGK To├Īn 11 K├¬╠üt n├┤╠üi tri thŲ░╠üc tß║Łp 1 - KNTT
Mß╗Öt quß║Ż b├│ng cao su ─æŲ░ß╗Żc thß║Ż tß╗½ ─æß╗Ö cao 5 m xuß╗æng mß╗Öt mß║Ęt s├Ān. Sau mß╗Śi lß║¦n chß║Īm s├Ān, quß║Ż b├│ng nß║Ży l├¬n ─æß╗Ö cao bß║▒ng 2323 ─æß╗Ö cao trŲ░ß╗øc ─æ├│. Giß║Ż sß╗Ł rß║▒ng quß║Ż b├│ng lu├┤n chuyß╗ān ─æß╗Öng vu├┤ng g├│c vß╗øi mß║Ęt s├Ān v├Ā qu├Ī tr├¼nh n├Āy tiß║┐p diß╗ģn v├┤ hß║Īn lß║¦n. Giß║Ż sß╗Ł \({{u_n}}\) l├Ā ─æß╗Ö cao (t├Łnh bß║▒ng m├®t) cß╗¦a quß║Ż b├│ng sau lß║¦n nß║Ży l├¬n thß╗® n. Chß╗®ng minh rß║▒ng d├Ży sß╗æ \(\left( {{u_n}} \right)\) c├│ giß╗øi hß║Īn l├Ā 0.
-
Hoß║Īt ─æß╗Öng 3 trang 106 SGK To├Īn 11 K├¬╠üt n├┤╠üi tri thŲ░╠üc tß║Łp 1 - KNTT
Cho hai d├Ży sß╗æ (\({u_n}\)┬Ł) v├Ā (\({v_n}\)┬Ł) vß╗øi \({u_n} = 2 + \frac{1}{n},{v_n} = 3 - \frac{2}{n}\).
T├Łnh v├Ā so s├Īnh: \(\mathop {\lim }\limits_{n \to + \infty } \left( {{u_n} + {v_n}} \right)\) v├Ā \(\mathop {\lim }\limits_{n \to + \infty } {u_n} + \mathop {\lim }\limits_{n \to + \infty } {v_n}\).
-
Luyß╗ćn tß║Łp 3 trang 107 SGK To├Īn 11 K├¬╠üt n├┤╠üi tri thŲ░╠üc tß║Łp 1 - KNTT
Tìm \(\mathop {\lim }\limits_{n \to + \infty } \frac{{\sqrt {2{n^2} + 1} }}{{n + 1}}\)
-
Hoß║Īt ─æß╗Öng 4 trang 107 SGK To├Īn 11 K├¬╠üt n├┤╠üi tri thŲ░╠üc tß║Łp 1 - KNTT
Cho h├¼nh vu├┤ng cß║Īnh 1 (─æŲĪn vß╗ŗ ─æß╗Ö d├Āi). Chia h├¼nh vu├┤ng ─æ├│ th├Ānh bß╗æn h├¼nh vu├┤ng nhß╗Å bß║▒ng nhau, sau ─æ├│ t├┤ m├Āu h├¼nh vu├┤ng nhß╗Å g├│c dŲ░ß╗øi b├¬n tr├Īi (H.5.2). Lß║Ęp lß║Īi c├Īc thao t├Īc n├Āy vß╗øi h├¼nh vu├┤ng nhß╗Å g├│c tr├¬n b├¬n phß║Żi. Giß║Ż sß╗Ł qu├Ī tr├¼nh tr├¬n tiß║┐p diß╗ģn v├┤ hß║Īn lß║¦n. Gß╗Źi u1, u2, ..., un, ... lß║¦n lŲ░ß╗Żt l├Ā ─æß╗Ö d├Āi cß║Īnh cß╗¦a c├Īc h├¼nh vu├┤ng ─æŲ░ß╗Żc t├┤ m├Āu.
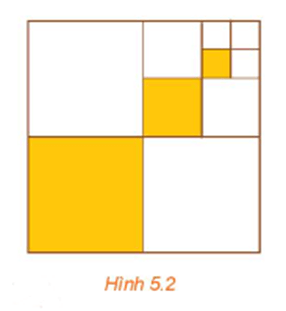
a) T├Łnh tß╗Ģng Sn = u1 + u2 + ... + un.
b) Tìm S =\(\mathop {\lim }\limits_{n \to + \infty } {S_n}\).
-
Luyß╗ćn tß║Łp 4 trang 108 SGK To├Īn 11 K├¬╠üt n├┤╠üi tri thŲ░╠üc tß║Łp 1 - KNTT
T├Łnh tß╗Ģng \(S = 2 + \frac{2}{7} + \frac{2}{{49}} + \ldots + \frac{2}{{{7^{n - 1}}}} + \ldots \)
-
Vß║Łn dß╗źng 2 trang 108 SGK To├Īn 11 K├¬╠üt n├┤╠üi tri thŲ░╠üc tß║Łp 1 - KNTT
─Éß╗ā ─æŲĪn giß║Żn, ta giß║Ż sß╗Ł Achilles chß║Īy vß╗øi vß║Łn tß╗æc 100km/h, vß║Łn tß╗æc cß╗¦a r├╣a l├Ā 1 km/h v├Ā khoß║Żng c├Īch ban ─æß║¦u a = 100(km)
a) T├Łnh thß╗Øi gian \({t_1},\:{t_2}, \ldots ,{t_n}, \ldots \) tŲ░ŲĪng ß╗®ng ─æß╗ā Achilles ─æi tß╗½ \({A_1}\) ─æß║┐n \({A_2}\), tß╗½ \({A_2}\) ─æß║┐n \({A_3}\),ŌĆ”, tß╗½ \({A_n}\) ─æß║┐n \({A_{n+1}}\),ŌĆ”
b) T├Łnh tß╗Ģng thß╗Øi gian cß║¦n thiß║┐t ─æß╗ā Achilles chß║Īy hß║┐t c├Īc qu├Żng ─æŲ░ß╗Øng \({A_1}{A_2},\:{A_2}{A_3}, \ldots ,\:{A_n}{A_{n + 1}}\),ŌĆ” tß╗®c l├Ā thß╗Øi gian cß║¦n thiß║┐t ─æß╗ā Achilles ─æuß╗Ģi kß╗ŗp r├╣a
c) Sai lß║¦m trong lß║Łp luß║Łn cß╗¦a Zeno l├Ā ß╗¤ ─æ├óu?
-
Hoß║Īt ─æß╗Öng 5 trang 108 SGK To├Īn 11 K├¬╠üt n├┤╠üi tri thŲ░╠üc tß║Łp 1 - KNTT
Mß╗Öt loß║Īi vi khuß║®n ─æŲ░ß╗Żc nu├┤i cß║źy vß╗øi sß╗æ lŲ░ß╗Żng ban ─æß║¦u l├Ā 50. Sau mß╗Śi chu k├¼ 4 giß╗Ø, sß╗æ lŲ░ß╗Żng cß╗¦a ch├║ng sß║Į t─āng gß║źp ─æ├┤i.
a) Dß╗▒ ─æo├Īn c├┤ng thß╗®c t├Łnh sß╗æ vi khuß║®n un sau chu k├¼ thß╗® n.
b) Sau bao l├óu, sß╗æ lŲ░ß╗Żng vi khuß║®n sß║Į vŲ░ß╗Żt con sß╗æ 10 000?
-
Luyß╗ćn tß║Łp 5 trang 109 SGK To├Īn 11 K├¬╠üt n├┤╠üi tri thŲ░╠üc tß║Łp 1 - KNTT
T├Łnh \(\mathop {\lim }\limits_{n \to + \infty } \left( {n - \sqrt n } \right)\).
-
Giß║Żi B├Āi 5.1 trang 109 SGK To├Īn 11 K├¬╠üt n├┤╠üi tri thŲ░╠üc tß║Łp 1 - KNTT
T├¼m c├Īc giß╗øi hß║Īn sau:
a) \(\mathop {lim}\limits_{n \to + \infty } \frac{{{n^2} + n + 1}}{{2{n^2} + 1}}\)
b) \(\mathop {lim}\limits_{n \to + \infty } \left( {\sqrt {{n^2} + 2n} - n} \right)\)
-
Giß║Żi B├Āi 5.2 trang 109 SGK To├Īn 11 K├¬╠üt n├┤╠üi tri thŲ░╠üc tß║Łp 1 - KNTT
Cho hai d├Ży sß╗æ kh├┤ng ├óm (un) v├Ā (vn) vß╗øi \(\mathop {\lim }\limits_{n \to + \infty } {u_n} = 2\) v├Ā \(\mathop {\lim }\limits_{n \to + \infty } {v_n} = 3\). T├¼m c├Īc giß╗øi hß║Īn sau:
a) \(\mathop {\lim }\limits_{n \to + \infty } \frac{{u_n^2}}{{{v_n} - {u_n}}}\);
b) \(\mathop {\lim }\limits_{n \to + \infty } \sqrt {{u_n} + 2{v_n}} \).
-
Giß║Żi B├Āi 5.3 trang 109 SGK To├Īn 11 K├¬╠üt n├┤╠üi tri thŲ░╠üc tß║Łp 1 - KNTT
T├¼m giß╗øi hß║Īn cß╗¦a c├Īc d├Ży sß╗æ cho bß╗¤i:
a) \({u_n} = \frac{{{n^2} + 1}}{{2n - 1}}\);
b) \({v_n} = \sqrt {2{n^2} + 1} - n\).
-
Giß║Żi B├Āi 5.4 trang 109 SGK To├Īn 11 K├¬╠üt n├┤╠üi tri thŲ░╠üc tß║Łp 1 - KNTT
Viß║┐t c├Īc sß╗æ thß║Łp ph├ón v├┤ hß║Īn tuß║¦n ho├Ān sau ─æ├óy dŲ░ß╗øi dß║Īng ph├ón sß╗æ:
a) 1,(12) = 1,121212...;
b) 3,(102) = 3,102102102...
-
Giß║Żi B├Āi 5.5 trang 109 SGK To├Īn 11 K├¬╠üt n├┤╠üi tri thŲ░╠üc tß║Łp 1 - KNTT
Mß╗Öt bß╗ćnh nh├ón h├Āng ng├Āy phß║Żi uß╗æng mß╗Öt vi├¬n thuß╗æc 150 mg. Sau ng├Āy ─æß║¦u, trŲ░ß╗øc mß╗Śi lß║¦n uß╗æng, h├Ām lŲ░ß╗Żng thuß╗æc c┼® trong cŲĪ thß╗ā vß║½n c├▓n 5%. T├Łnh lŲ░ß╗Żng thuß╗æc c├│ trong cŲĪ thß╗ā sau khi uß╗æng vi├¬n thuß╗æc cß╗¦a ng├Āy thß╗® 5. Ų»ß╗øc t├Łnh lŲ░ß╗Żng thuß╗æc trong cŲĪ thß╗ā nß║┐u bß╗ćnh nh├ón sß╗Ł dß╗źng thuß╗æc trong mß╗Öt thß╗Øi gian d├Āi.
-
Giß║Żi B├Āi 5.6 trang 109 SGK To├Īn 11 K├¬╠üt n├┤╠üi tri thŲ░╠üc tß║Łp 1 - KNTT
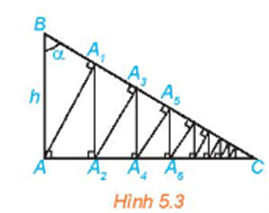
Cho tam gi├Īc vu├┤ng ABC vu├┤ng tß║Īi A, c├│ AB = h v├Ā g├│c B bß║▒ng ╬▒ (H.5.3). Tß╗½ A kß║╗ \(A{A_1} \bot BC\), tß╗½ A1 kß║╗ \({A_1}{A_2} \bot AC\), sau ─æ├│ lß║Īi kß║╗ \({A_2}{A_3} \bot BC\). Tiß║┐p tß╗źc qu├Ī tr├¼nh tr├¬n, ta ─æŲ░ß╗Żc ─æŲ░ß╗Øng gß║źp kh├║c v├┤ hß║Īn \(A{A_1}{A_2}{A_3} \ldots \) T├Łnh ─æß╗Ö d├Āi ─æŲ░ß╗Øng gß║źp kh├║c n├Āy theo h v├Ā ╬▒
-
Ba╠Ći t├ó╠Żp 5.1 trang 77 SBT Toa╠ün 11 T├ó╠Żp 1 K├¬╠üt n├┤╠üi tri thŲ░╠üc - KNTT
T├Łnh c├Īc giß╗øi hß║Īn sau:
a) \(\mathop {\lim }\limits_{n \to + \infty } \frac{{{n^2} + 1}}{{2{n^2} + n + 2}};\)
b) \(\mathop {\lim }\limits_{n \to + \infty } \frac{{{2^n} + 3}}{{1 + {3^n}}}.\)
-
Ba╠Ći t├ó╠Żp 5.2 trang 78 SBT Toa╠ün 11 T├ó╠Żp 1 K├¬╠üt n├┤╠üi tri thŲ░╠üc - KNTT
T├Łnh c├Īc giß╗øi hß║Īn sau:
a) \(\mathop {\lim }\limits_{n \to + \infty } \left( {\sqrt {{n^2} + 2n} - n - 2} \right);\)
b) \(\mathop {\lim }\limits_{n \to + \infty } \left( {2 + {n^2} - \sqrt {{n^4} + 1} } \right);\)
c) \(\mathop {\lim }\limits_{n \to + \infty } \left( {\sqrt {{n^2} - n + 2} + n} \right);\)
d) \(\mathop {\lim }\limits_{n \to + \infty } \left( {3n - \sqrt {4{n^2} + 1} } \right).\)
-
Ba╠Ći t├ó╠Żp 5.3 trang 78 SBT Toa╠ün 11 T├ó╠Żp 1 K├¬╠üt n├┤╠üi tri thŲ░╠üc - KNTT
Cho \({u_n} = \frac{{1 + a + {a^2} + ... + {a^n}}}{{1 + b + {b^2} + ... + {b^n}}}\) vß╗øi a, b l├Ā c├Īc sß╗æ thß╗▒c thß╗Åa m├Żn \(\left| a \right| < 1,\left| b \right| < 1\). T├¼m \(\mathop {\lim }\limits_{n \to + \infty } {u_n}\)?
-
Ba╠Ći t├ó╠Żp 5.4 trang 78 SBT Toa╠ün 11 T├ó╠Żp 1 K├¬╠üt n├┤╠üi tri thŲ░╠üc - KNTT
Tìm \(\mathop {\lim }\limits_{n \to + \infty } \frac{{1 + 3 + 5 + ... + \left( {2n - 1} \right)}}{{{n^2} + 2n}}\)?
-
Ba╠Ći t├ó╠Żp 5.5 trang 78 SBT Toa╠ün 11 T├ó╠Żp 1 K├¬╠üt n├┤╠üi tri thŲ░╠üc - KNTT
T├Łnh tß╗Ģng \(S = - 1 + \frac{1}{5} - \frac{1}{{{5^2}}} + ... + {\left( { - 1} \right)^n}\frac{1}{{{5^{n - 1}}}} + ...\)?
-
Ba╠Ći t├ó╠Żp 5.6 trang 78 SBT Toa╠ün 11 T├ó╠Żp 1 K├¬╠üt n├┤╠üi tri thŲ░╠üc - KNTT
Viß║┐t c├Īc sß╗æ thß║Łp ph├ón v├┤ hß║Īn tuß║¦n ho├Ān sau dŲ░ß╗øi dß║Īng ph├ón sß╗æ:
a) 1,(03);
b) 3,(23).
-
Ba╠Ći t├ó╠Żp 5.7 trang 78 SBT Toa╠ün 11 T├ó╠Żp 1 K├¬╠üt n├┤╠üi tri thŲ░╠üc - KNTT
Cho d├Ży sß╗æ \(\left( {{u_n}} \right)\) vß╗øi \({u_n} = \frac{{\cos n}}{{{n^2}}}.\) T├¼m \(\mathop {\lim }\limits_{n \to + \infty } {u_n}\)?
-
Ba╠Ći t├ó╠Żp 5.8 trang 78 SBT Toa╠ün 11 T├ó╠Żp 1 K├¬╠üt n├┤╠üi tri thŲ░╠üc - KNTT
Cho tam gi├Īc \({A_1}{B_1}{C_1}\) c├│ diß╗ćn t├Łch l├Ā 3 (─æŲĪn vß╗ŗ diß╗ćn t├Łch). Dß╗▒ng tam gi├Īc \({A_2}{B_2}{C_2}\) bß║▒ng c├Īch nß╗æi c├Īc trung ─æiß╗ām cß╗¦a c├Īc cß║Īnh \({B_1}{C_1},{C_1}{A_1},{A_1}{B_1}.\) Tiß║┐p tß╗źc qu├Ī tr├¼nh n├Āy, ta c├│ c├Īc tam gi├Īc \({A_3}{B_3}{C_3},...,{A_n}{B_n}{C_n},...\) K├Ł hiß╗ću \({s_n}\) l├Ā diß╗ćn t├Łch cß╗¦a tam gi├Īc \({A_n}{B_n}{C_n}\).
a) T├Łnh \({s_n}\)?
b) T├Łnh tß╗Ģng \({s_1} + {s_2} + ... + {s_n} + ...\)?
-
Ba╠Ći t├ó╠Żp 5.9 trang 78 SBT Toa╠ün 11 T├ó╠Żp 1 K├¬╠üt n├┤╠üi tri thŲ░╠üc - KNTT
Cho d├Ży sß╗æ \(\left( {{u_n}} \right)\) vß╗øi \({u_1} = 2,{u_{n + 1}} = {u_n} + \frac{2}{{{3^n}}},n \ge 1\). ─Éß║Ęt \({v_n} = {u_{n + 1}} - {u_n}.\)
a) T├Łnh \({v_1} + {v_2} + ... + {v_n}\) theo n.
b) T├Łnh \({u_n}\) theo n.
c) Tìm \(\mathop {\lim }\limits_{n \to + \infty } {u_n}\)
-
Ba╠Ći t├ó╠Żp 5.10 trang 78 SBT Toa╠ün 11 T├ó╠Żp 1 K├¬╠üt n├┤╠üi tri thŲ░╠üc - KNTT
Cho d├Ży sß╗æ \(\left( {{u_n}} \right)\) c├│ t├Łnh chß║źt \(\left| {{u_n} - \frac{n}{{n + 1}}} \right| \le \frac{1}{{{n^2}}}\). T├Łnh \(\mathop {\lim }\limits_{n \to + \infty } {u_n}\)?






