Hướng dẫn Giải bài tập Toán 11 Chân trời sáng tạo Chương 3 Bài 1 Giới hạn của dãy số môn Toán lớp 11 giúp các em học sinh nắm vững phương pháp giải bài tập và ôn luyện tốt kiến thức.
-
Hoạt động khởi động trang 64 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Bạn nam thứ 1: Số thập phân vô hạn tuần hoàn 0,666... và số là hai số bằng nhau.
Bạn nam thứ 2: Không thể như vậy được, vì 0,6 < ; 0,66 < ; 0,666 < ; ...
Bạn nữ: ???
-
Hoạt động khám phá 1 trang 64 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Cho dãy số \(\left( {{u_n}} \right)\) với .\({u_n} = \frac{{{{\left( { - 1} \right)}^n}}}{n}\).
a) Tìm các giá trị còn thiếu trong bảng sau:
.png)
b) Với \(n\) thế nào thì \(\left| {{u_n}} \right|\) bé hơn 0,01; 0,001?
c) Một số số hạng của dãy số được biểu diễn trên trục số như Hình 1.

Từ các kết quả trên, có nhận xét gì về khoảng cách từ điểm \({u_n}\) đến điểm 0 khi \(n\) trở nên rất lớn?
-
Thực hành 1 trang 65 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Tính các giới hạn sau:
a) \(\lim \frac{1}{{{n^2}}}\);
b) \(\lim {\left( { - \frac{3}{4}} \right)^n}\).
-
Hoạt động khám phá 2 trang 65 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Cho dãy số \(\left( {{u_n}} \right)\) với \({u_n} = \frac{{2n + 1}}{n}\).
a) Cho dãy số \(\left( {{v_n}} \right)\) với \({v_n} = {u_n} - 2\). Tìm giới hạn \(\lim {v_n}\).
b) Biểu diễn các điểm \({u_1},{u_2},{u_3},{u_4}\) trên trục số. Có nhận xét gì về vị trí của các điểm \({u_n}\) khi \(n\) trở nên rất lớn?
-
Thực hành 2 trang 65 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Tìm các giới hạn sau:
a) \(\lim \left( {2 + {{\left( {\frac{2}{3}} \right)}^n}} \right)\);
b) \(\lim \left( {\frac{{1 - 4n}}{n}} \right)\).
-
Hoạt động khám phá 3 trang 66 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Ở trên ta đã biết \(\lim \left( {3 + \frac{1}{{{n^2}}}} \right) = \lim \frac{{3{n^2} + 1}}{{{n^2}}} = 3\).
a) Tìm các giới hạn \(\lim 3\) và \(\lim \frac{1}{{{n^2}}}\).
b) Từ đó, nêu nhận xét về \(\lim \left( {3 + \frac{1}{{{n^2}}}} \right)\) và \(\lim 3 + \lim \frac{1}{{{n^2}}}\).
-
Thực hành 3 trang 66 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Tìm các giới hạn sau:
a) \(\lim \frac{{2{n^2} + 3n}}{{{n^2} + 1}}\)
b) \(\lim \frac{{\sqrt {4{n^2} + 3} }}{n}\)
-
Hoạt động khám phá 4 trang 67 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Từ một hình vuông có cạnh bằng 1, tô màu một nửa hình vuông, rồi tô màu một nửa hình còn lại và cứ tiếp tục như vậy (xem Hình 2).
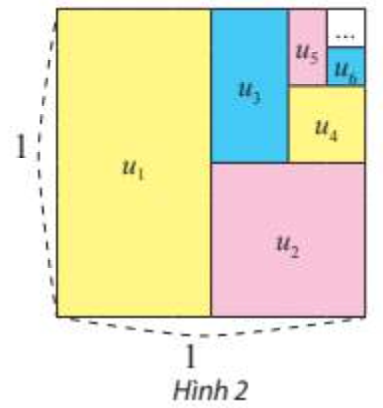
a) Xác định diện tích \({u_k}\) của phần hình được tô màu lần thứ \(k\left( {k = 1,2,3,...} \right)\).
b) Tính tổng diện tính \({S_n}\) của phần hình được tô màu sau lần tô thứ \(n\left( {n = 1,2,3,...} \right)\).
c) Tìm giới hạn \(\lim {S_n}\) và so sánh giới hạn này với diện tích hình vuông ban đầu.
-
Thực hành 4 trang 68 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Tính tổng của cấp số nhân lùi vô hạn: \(1 + \frac{1}{3} + {\left( {\frac{1}{3}} \right)^2} + ... + {\left( {\frac{1}{3}} \right)^n} + ...\).
-
Vận dụng 1 trang 68 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
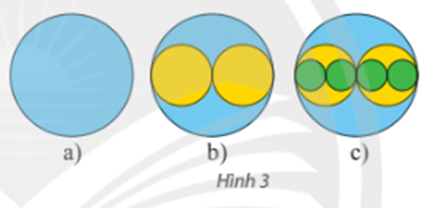
Từ tờ giấy, cắt một hình tròn bán kính \(R\left( {cm} \right)\) như Hình 3a. Tiếp theo, cắt hai hình tròn bán kính \(\frac{R}{2}\) rồi chồng lên hình tròn đầu tiên như Hình 3b. Tiếp theo, cắt bốn hình tròn bán kính \(\frac{R}{4}\) rồi chồng lên các hình trước như Hình 3c. Cứ thế tiếp tục mãi. Tính tổng diện tích của các hình tròn.
-
Hoạt động khám phá 5 trang 68 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
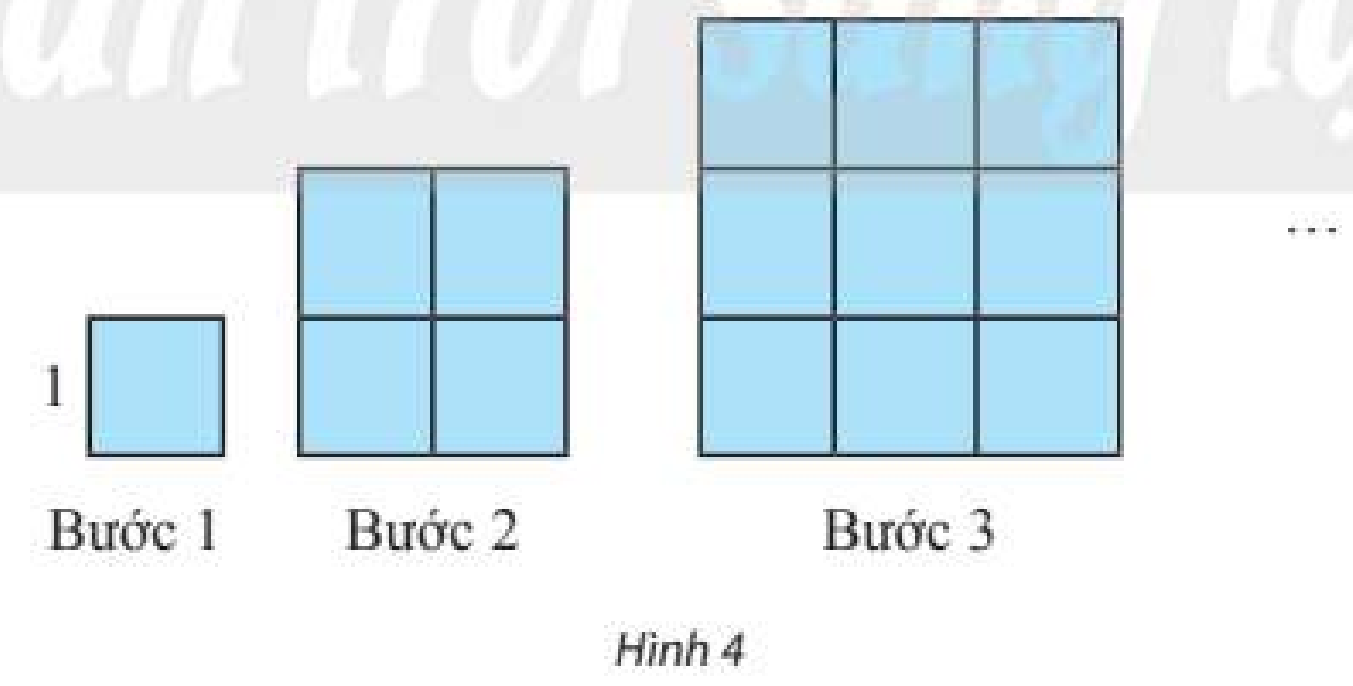
Dựng một dãy hình vuông bằng cách ghép từ các hình vuông đơn vị (cạnh bằng 1 đơn vị độ dài) theo các bước như Hình 4. Kí hiệu \({u_n}\) (đơn vị diện tích) là diện tích hình vuông dựng được ở bước thứ \(n\).
a) Với \(n\) như thế nào thì \({u_n}\) vượt quá 10000; 1000000?
b) Cho hình có diện tích \(S\). Với \(n\) như thế nào thì \({u_n}\) vượt quá \(S\)?
-
Giải Bài 1 trang 69 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Tìm các giới hạn sau:
a) \(\lim \frac{{ - 2n + 1}}{n}\)
b) \(\lim \frac{{\sqrt {16{n^2} - 2} }}{n}\)
c) \(\lim \frac{4}{{2n + 1}}\)
d) \(\lim \frac{{{n^2} - 2n + 3}}{{2{n^2}}}\)
-
Giải Bài 2 trang 69 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Tính tổng của các cấp số nhân lùi vô hạn sau:
a) \( - \frac{1}{2} + \frac{1}{4} - \frac{1}{8} + ... + {\left( { - \frac{1}{2}} \right)^n} + ...\)
b) \(\frac{1}{4} + \frac{1}{{16}} + \frac{1}{{64}} + ... + {\left( {\frac{1}{4}} \right)^n} + ...\)
-
Giải Bài 3 trang 69 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Viết số thập phân vô hạn tuần hoàn \(0,444...\) dưới dạng một phân số.
-
Giải Bài 4 trang 70 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
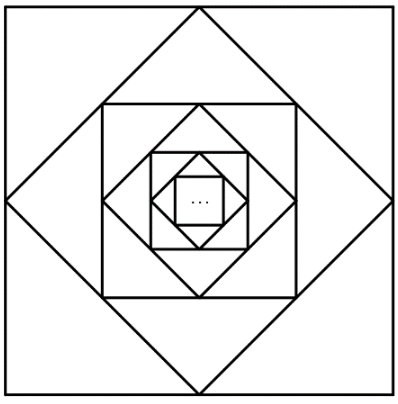
Từ hình vuông đầu tiên có cạnh bằng 1 (đơn vị độ dài), nối các trung điểm của bốn cạnh để có hình vuông thứ hai. Tiếp tục nối các trung điểm của bốn cạnh của hình vuông thứ hai để được hình vuông thứ ba. Cứ tiếp tục làm như thế, nhận được một dãy hình vuông (xem Hình 5).
a) Kí hiệu \({a_n}\) là diện tích của hình vuông thứ \(n\) và \({S_n}\) là tổng diện tích của \(n\) hình vuông đầu tiên. Viết công thức tính \({a_n},{S_n}\left( {n = 1,2,3,...} \right)\) và tìm \(\lim {S_n}\) (giới hạn này nếu có được gọi là tổng diện tích của các hình vuông).
b) Kí hiệu \({p_n}\) là chu vi của hình vuông thứ \(n\) và \({Q_n}\) là tổng chu vi của \(n\) hình vuông đầu tiên. Viết công thức tính \({p_n}\) và \({Q_n}\left( {n = 1,2,3,...} \right)\) và tìm \(\lim {Q_n}\) (giới hạn này nếu có được gọi là tổng chu vi của các hình vuông).
-
Giải Bài 5 trang 70 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Xét quá trình tạo ra hình có chu vi vô cực và diện tích bằng 0 như sau:
Bắt đầu bằng một hình vuông \({H_0}\) cạnh bằng 1 đơn vị độ dài (xem Hình 6a). Chia hình vuông \({H_0}\) thành chính hình vuông bằng nhau, bỏ đi bốn hình vuông, nhận được hình \({H_1}\) (xem Hình 6b). Tiếp theo, chia mỗi hình vuông của \({H_1}\) thành chín hình vuông, rồi bỏ đi bốn hình vuông, nhận được hình \({H_2}\) (xem Hình 6c). Tiếp tục quá trình này, ta nhận được một dãy hình \({H_n}\left( {n = 1,2,3,...} \right)\).
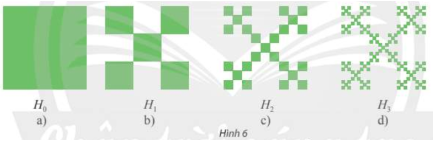
Ta có: \({H_1}\) có 5 hình vuông, mỗi hình vuông có cạnh bằng \(\frac{1}{3}\);
\({H_2}\) có \(5.5 = {5^2}\) hình vuông, mỗi hình vuông có cạnh bằng \(\frac{1}{3}.\frac{1}{3} = \frac{1}{{{3^2}}}\);…
Từ đó, nhận được hình \({H_n}\) có \({5^n}\) hình vuông, mỗi hình vuông có cạnh bằng \(\frac{1}{{{3^n}}}\).
a) Tính diện tích \({S_n}\) của \({H_n}\) và tính \(\lim {S_n}\).
b) Tính chu vi \({p_n}\) của \({H_n}\) và tính \(\lim {p_n}\).
(Quá trình trên tạo nên một hình, gọi là một fractal, được coi là có diện tích \(\lim {S_n}\) và chu vi \(\lim {p_n}\)).
-
Bài tập 1 trang 75 SBT Toán 11 Tập 1 Chân trời sáng tạo - CTST
Tìm các giới hạn sau:
a)
b)
c)
d)
-
Bài tập 2 trang 75 SBT Toán 11 Tập 1 Chân trời sáng tạo - CTST
Tìm các giới hạn sau:
a)
b)
c)
d)
e)
g)
-
Bài tập 3 trang 75 SBT Toán 11 Tập 1 Chân trời sáng tạo - CTST
Tìm các giới hạn sau:
a)
b)
c)
d)
-
Bài tập 4 trang 76 SBT Toán 11 Tập 1 Chân trời sáng tạo - CTST
Cho hai dãy số (un) và (vn) có limun = 3, limvn = 4. Tìm các giới hạn sau:
a) lim(3un ‒ 4);
b) lim(un + 2vn);
c) lim(un ‒ vn)2;
d) .
-
Bài tập 5 trang 76 SBT Toán 11 Tập 1 Chân trời sáng tạo - CTST
Cho dãy số (un) thoả mãn \(lim(n.u_{n}) = 3\). Tìm giới hạn ?
-
Bài tập 6 trang 76 SBT Toán 11 Tập 1 Chân trời sáng tạo - CTST
Tìm các giới hạn sau:
a) lim(1 + 3n – n2);
b)
c)
d) lim(3n+1 – 5n).
-
Bài tập 7 trang 76 SBT Toán 11 Tập 1 Chân trời sáng tạo - CTST
Tuỳ theo giá trị của a > 0, tìm giới hạn ?
-
Bài tập 8 trang 76 SBT Toán 11 Tập 1 Chân trời sáng tạo - CTST
Tính tổng của các cấp số nhân lùi vô hạn:
a)
b)
-
Bài tập 9 trang 76 SBT Toán 11 Tập 1 Chân trời sáng tạo - CTST
Viết các số thập phân vô hạn tuần hoàn sau thành phân số:
a) 0,(7) = 0,777...;
b) 1,(45) = 1,454545...
-
Bài tập 10 trang 76 SBT Toán 11 Tập 1 Chân trời sáng tạo - CTST
Tại một nhà máy, người ta đo được rằng 80% lượng nước sau khi sử dụng được xử lí và tái sử dụng. Với 100 m3 ban đầu được sử dụng lần đầu tại nhà máy, khi quá trình xử lí và tái sử dụng lặp lại mãi mãi, nhà máy sử dụng được tổng lượng nước là bao nhiêu?
-
Bài tập 11 trang 76 SBT Toán 11 Tập 1 Chân trời sáng tạo - CTST
Cho tam giác OA1A2 vuông cân tại A2 có cạnh huyền OA1 bằng a. Bên ngoài tam giác OA1A2, vẽ tam giác OA2A3 vuông cân tại A3. Tiếp theo, bên ngoài tam giác OA2A3, vẽ tam giác OA3A4 vuông cân tại A4. Cứ tiếp tục quá trình như trên, ta vẽ được một dãy các hình tam giác vuông cân (Hình 2). Tính độ dài đường gấp khúc A1A2A3A4...?
-
Bài tập 12 trang 77 SBT Toán 11 Tập 1 Chân trời sáng tạo - CTST
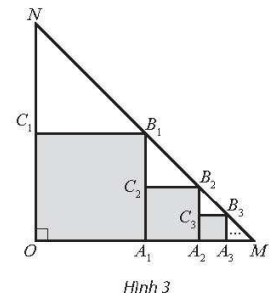
Cho tam giác OMN vuông cân tại O, OM = ON = 1. Trong tam giác OMN, vẽ hình vuông OA1B1C1 sao cho các đỉnh A1, B1, C1 lần lượt nằm trên các cạnh OM, MN, ON. Trong tam giác A1MB1, vẽ hình vuông A1A2B2C2 sao cho các đỉnh A2, B2, C2 lần lượt nằm trên các cạnh A1M, MB1, A1B1. Tiếp tục quá trình đó, ta được một dãy các hình vuông (Hình 3). Tính tổng diện tích các hình vuông này?
-
Bài tập 13 trang 77 SBT Toán 11 Tập 1 Chân trời sáng tạo - CTST
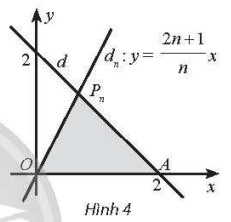
Trong mặt phẳng toạ độ Oxy, đường thẳng d: x + y = 2 cắt trục hoành tại điểm A và cắt đường thẳng tại điểm Pn (n ∈ ℕ*). Kí hiệu Sn là diện tích của tam giác OAPn. Tìm \(lim(S_n)\)?

.PNG)





