Bài tập 13 trang 77 SBT Toán 11 Tập 1 Chân trời sáng tạo
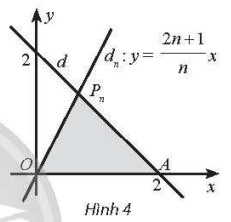
Trong mặt phẳng toạ độ Oxy, đường thẳng d: x + y = 2 cắt trục hoành tại điểm A và cắt đường thẳng tại điểm Pn (n ∈ ℕ*). Kí hiệu Sn là diện tích của tam giác OAPn. Tìm \(lim(S_n)\)?
Hướng dẫn giải chi tiết Bài tập 13
Ta có: A(2; 0) nên OA = 2.
Đường thẳng d: x + y = 2 ⇔ y = 2 – x.
Vì Pn (x0; y0) ∈ d nên Pn (x0; 2 – x0)
Hơn nữa Pn(x0; y0) ∈ dn nên ta có:
Gọi H là hình chiếu của Pn lên Ox.
Khi đó PnH = |y0| = (do n ∈ ℕ*).
Ta có Sn =
Khi đó
-- Mod Toán 11 HỌC247
Chưa có câu hỏi nào. Em hãy trở thành người đầu tiên đặt câu hỏi.





