Nội dung bài học Khoảng cách trong chương trình Toán lớp 11 của Kết Nối Tri Thức sẽ giúp các em học sinh nắm được khái niệm về khoảng cách giữa các đối tượng trong không gian và phương pháp để xác định khoảng cách giữa chúng. Bên cạnh đó, bài học cũng cung cấp các ví dụ minh họa giúp các em phát triển kỹ năng giải các bài tập liên quan đến khoảng cách.
Tóm tắt lý thuyết
1.1. Khoảng cách từ một điểm đến một đường thẳng, đến một mặt phẳng
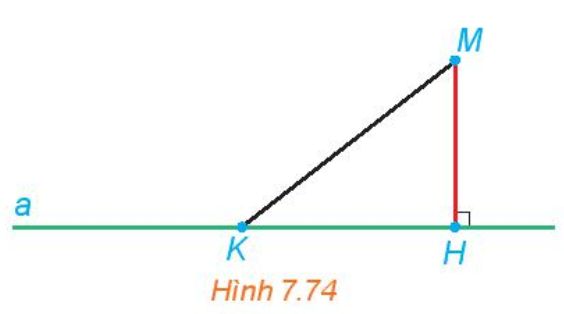
| Khoảng cách từ một điểm M đến một đường thẳng a, kí hiệu d(M, a), là khoảng cách giữa M và hình chiếu H của M trên a. |
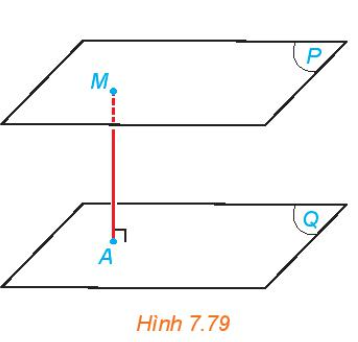
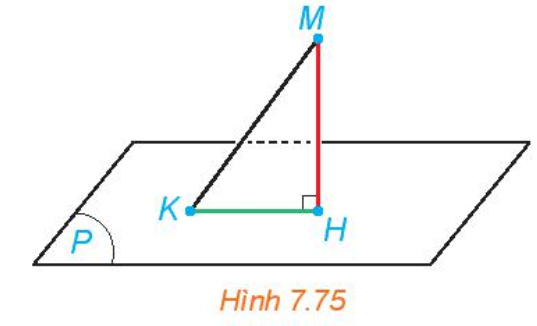
| Khoảng cách từ một điểm M đến một mặt phẳng (P), kí hiệu d(M, (P)), là khoảng cách giữa M và hình chiếu H của M trên (P). |
Chú ý: d(M, a) = 0 khi và chỉ khi M \(\in\) a và d(M, (P)) = 0 khi và chỉ khi M \(\in\) (P).
Nhận xét: Khoảng cách từ M đến đường thẳng a (mặt phẳng (P)) là khoảng cách nhỏ nhất giữa M và một điểm thuộc a (thuộc (P)).
Chú ý: Khoảng cách từ đỉnh đến mặt phẳng chứa mặt đáy của một hình chóp được gọi là chiều cao của hình chóp đó.
1.2. Khoảng cách giữa các đường thẳng và mặt phẳng song song, giữa hai mặt phẳng song song
| Khoảng cách giữa đường thẳng a và mặt phẳng (P) song song với a, kí hiệu d(a, (P)). là khoảng cách từ một điểm bất kì trên a đến (P). |
|
Khoảng cách giữa hai mặt phẳng song song (P) và (Q), kí hiệu d((P), (Q)), là khoảng cách từ một điềm bất kì thuộc mặt phẳng này đến mặt phẳng kia. Khoảng cách giữa hai đường thẳng song song m và n, kí hiệu d(m, n), là khoảng cách từ một điểm thuộc đường thẳng này đến đường thằng kia. |
Chú ý: Khoảng cách giữa hai đáy của một hình lăng trụ được gọi là chiều cao của hình lăng trụ đó.
1.3. Khoảng cách giữa hai đường thẳng chéo nhau
|
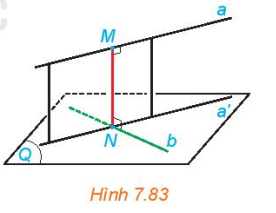
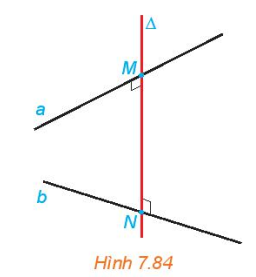
Đường thằng \(\Delta\) cắt hai đường thẳng chéo nhau a, b và vuông góc với cả hai đường thẳng đó được gọi là đường vuông góc chung của a và b. |
|
Nếu đường vuông góc chung \(\Delta\) cắt a, b tương ứng tại M, N thì độ dài đoạn thẳng MN được gọi là khoảng cách giữa hai đường thẳng chéo nhau a, b. |
Nhận xét
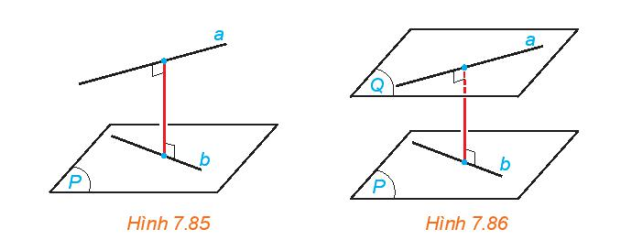
- Khoảng cách giữa hai đường thẳng chéo nhau bằng khoảng cách giữa một trong hai đường thẳng đó đến mặt phẳng song song với nó và chứa đường thẳng còn lại (H.7.85).
- Khoảng cách giữa hai đường thẳng chéo nhau bằng khoảng cách giữa hai mặt phẳng song song, tương ứng chứa hai đường thẳng đó (H.7,86).
Bài tập minh họa
Câu 1:
Cho mặt phẳng \(\left (\alpha \right )\), điểm A không thuộc mặt phẳng \(\left (\alpha \right )\), H là hình chiếu vuông góc của A lên mặt phẳng \(\left (\alpha \right )\), E là điểm thuộc AM sao cho: \(\frac{{ME}}{{MA}} = k.\)
a. Tính khoảng cách từ A đến mặt phẳng \(\left (\alpha \right )\).
b. Tính khoảng cách từ E đến mặt phẳng \(\left (\alpha \right )\), từ đó suy ra khoảng cách từ I – trung điểm của AM đến mặt phẳng \(\left (\alpha \right )\).
c. Gọi d là đường thẳng qua I song song với mặt phẳng \(\left (\alpha \right )\). Lấy J thuộc d, tính khoảng cách từ J đến mặt phẳng \(\left (\alpha \right )\).
d. Gọi C là chân đường vuông góc của J lên mặt phẳng \(\left (\alpha \right )\). D là trung điểm của JC. Tính khoảng cách từ D đến mặt phẳng \(\left (\alpha \right )\).
Hướng dẫn giải:
.png)
a) H là hình chiếu vuông góc của A lên mặt phẳng \(\left (\alpha \right )\) nên: d(A,\(\left (\alpha \right )\)) = AH = h.
b) Gọi P là chân đường vuông góc của E lên mặt phẳng \(\left (\alpha \right )\).
Khi đó: d(E, \(\left (\alpha \right )\)) = EP.
Ta có : EP // AH (đều vuông góc với mp \(\left (\alpha \right )\)) và M, P, H thẳng hàng.
Theo định lí Tallet ta có:
\(\frac{{EP}}{{AH}} = \frac{{ME}}{{MA}}=k\)
Khi đó: EP = k.AH hay d(E, (a)) = k.h (1).
Vì I là trung điểm của AM nên:
\(d(I,\left( \alpha \right)) = \frac{1}{2}.h\) (áp dụng kết quả (1) với \(k=\frac{1}{2}\)).
c) Ta có: IJCQ là hình chữ nhật nên IQ=JC
Do đó: \(d(J,\left( \alpha \right)) = d(I,\left( \alpha \right)) = \frac{1}{2}.h.\)
d) D là trung điểm của JC nên \(\frac{CD}{CJ}=\frac{1}{2}.\)
Suy ra: \(d(Q,\left( \alpha \right)) = \frac{1}{2}d(J,\left( \alpha \right)) = \frac{1}{2}.\frac{1}{2}.h = \frac{1}{4}.h\).
Câu 2:
Cho tứ diện SABC có tam giác ABC vuông cân đỉnh B, AB = a, SA vuông góc với mặt phẳng (ABC) và SA = a.
a. Chứng minh (SAB) \(\bot\) (SBC) .
b. Tính khoảng cách từ điểm A đến mp(SBC).
c. Gọi I là trung điểm của AB. Tính khoảng cách từ điểm I đến mp(SBC).
Hướng dẫn giải:
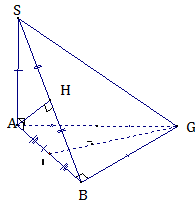
a) Theo giả thiết ta có: \(SA \bot (ABC)\).
Suy ra \(SA \bot BC\) (1).
Mà \(AB \bot BC\) (giả thiết) (2).
Từ (1) và (2) ta suy ra: \(BC \bot (SAB)\Rightarrow (SBC) \bot (SAB).\)
b) Ta có: \((SAB)\cap (SBC)=SB\).
Kẻ \(AH \bot SB (H\in SB).\)
Do tam giác SAB vuông cân nên H là trung điểm của SB.
Khi đó: \(AH \bot (SBC)\) nên \(d(A, (SBC))=AH\).
Xét tam giác SAB vuông cân tại A. Theo hệ thức lượng trong tam giác vuông ta có:
\(\frac{1}{{A{H^2}}} = \frac{1}{{A{S^2}}} + \frac{1}{{A{B^2}}} = \frac{1}{{{a^2}}} + \frac{1}{{{a^2}}} \Rightarrow AH = \frac{{a\sqrt 2 }}{2}.\)
c) Ta có: \(AB\cap (SBC)=B\) và \(\frac{BI}{BA}=\frac{1}{2}\) (do I là trùng điểm của AB) nên:
\(d(I,(SBC)) = \frac{1}{2}d(A,(SBC)) = \frac{1}{2}.\frac{{a\sqrt 2 }}{2} = \frac{{a\sqrt 2 }}{4}.\)
Luyện tập Bài 26 Toán 11 Kết Nối Tri Thức
Học xong bài học này, em có thể:
- Xác định khoảng cách giữa các đối tượng điểm, đường thẳng, mặt phẳng trong không gian.
- Xác định đường vuông góc chung của hai đường thẳng chéo nhau trong các trường hợp đơn giản. Vận dụng kiến thức về khoảng cách vào một số tinh huống thực tế.
3.1. Trắc nghiệm Bài 26 Toán 11 Kết Nối Tri Thức
Các em có thể hệ thống lại nội dung kiến thức đã học được thông qua bài kiểm tra Trắc nghiệm Toán 11 Kết nối tri thức Chương 7 Bài 26 cực hay có đáp án và lời giải chi tiết.
-
- A. Nếu hai đường thẳng a và b chéo nhau và vuông góc với nhau thì đường thẳng vuông góc chung của chúng nằm trong mặt phẳng (P) chứa đường thẳng này và vuông góc với đường thẳng kia.
- B. Khoảng cách giữa đường thẳng a và mặt phẳng (P) song song với a là khoảng cách từ một điểm A bất kỳ thuộc a tới mặt phẳng (P).
- C. Khoảng cách giữa hai đường thẳng chéo nhau a và b là khoảng cách từ một điểm M thuộc mặt phẳng (P) chứa a và song song với b đến một điểm N bất kỳ trên b.
- D. Khoảng cách giữa hai mặt phẳng song song là khoảng cách từ một điểm M bất kỳ trên mặt phẳng này đến mặt phẳng kia.
-
- A. MN
- B. AM
- C. BM
- D. AD
-
- A. Đường vuông góc chung của hai đường thẳng chéo nhau thì vuông góc với mặt phẳng chứa đường thẳng này và song song với đường thẳng kia.
- B. Một đường thẳng là đường vuông góc chung của hai đường thẳng chéo nhau nếu nó vuông góc với cả hai đường thẳng đó.
- C. Đường vuông góc chung của hai đường thẳng chéo nhau thì nằm trong mặt phẳng chứa đường thẳng này và vuông góc với đường thẳng kia.
- D. Một đường thẳng là đường vuông góc chung của hai đường thẳng chéo nhau nếu nó cắt cả hai đường thẳng đó.
Câu 4-10: Mời các em đăng nhập xem tiếp nội dung và thi thử Online để củng cố kiến thức về bài học này nhé!
3.2. Bài tập SGK Bài 26 Toán 11 Kết Nối Tri Thức
Các em có thể xem thêm phần hướng dẫn Giải bài tập Toán 11 Kết nối tri thức Chương 7 Bài 26 để giúp các em nắm vững bài học và các phương pháp giải bài tập.
Hoạt động 1 trang 54 SGK Toán 11 Kết nối tri thức tập 2 - KNTT
Luyện tập 1 trang 55 SGK Toán 11 Kết nối tri thức tập 2 - KNTT
Hoạt động 2 trang 55 SGK Toán 11 Kết nối tri thức tập 2 - KNTT
Hoạt động 3 trang 56 SGK Toán 11 Kết nối tri thức tập 2 - KNTT
Luyện tập 2 trang 56 SGK Toán 11 Kết nối tri thức tập 2 - KNTT
Vận dụng trang 57 SGK Toán 11 Kết nối tri thức tập 2 - KNTT
Hoạt động 4 trang 57 SGK Toán 11 Kết nối tri thức tập 2 - KNTT
Khám phá trang 58 SGK Toán 11 Kết nối tri thức tập 2 - KNTT
Giải Bài 7.22 trang 59 SGK Toán 11 Kết nối tri thức tập 2 - KNTT
Giải Bài 7.23 trang 59 SGK Toán 11 Kết nối tri thức tập 2 - KNTT
Giải Bài 7.24 trang 59 SGK Toán 11 Kết nối tri thức tập 2 - KNTT
Giải Bài 7.25 trang 59 SGK Toán 11 Kết nối tri thức tập 2 - KNTT
Giải Bài 7.26 trang 59 SGK Toán 11 Kết nối tri thức tập 2 - KNTT
Giải Bài 7.27 trang 59 SGK Toán 11 Kết nối tri thức tập 2 - KNTT
Bài tập 7.27 trang 37 SBT Toán 11 Tập 2 Kết nối tri thức - KNTT
Bài tập 7.28 trang 38 SBT Toán 11 Tập 2 Kết nối tri thức - KNTT
Bài tập 7.29 trang 38 SBT Toán 11 Tập 2 Kết nối tri thức - KNTT
Bài tập 7.30 trang 38 SBT Toán 11 Tập 2 Kết nối tri thức - KNTT
Bài tập 7.31 trang 38 SBT Toán 11 Tập 2 Kết nối tri thức - KNTT
Bài tập 7.32 trang 38 SBT Toán 11 Tập 2 Kết nối tri thức - KNTT
Hỏi đáp Bài 26 Toán 11 Kết Nối Tri Thức
Trong quá trình học tập nếu có thắc mắc hay cần trợ giúp gì thì các em hãy comment ở mục Hỏi đáp, Cộng đồng Toán học HOC247 sẽ hỗ trợ cho các em một cách nhanh chóng!
Chúc các em học tập tốt và luôn đạt thành tích cao trong học tập!
-- Mod Toán Học 11 HỌC247


.PNG)