Luyện tập 1 trang 55 SGK Toán 11 Kết nối tri thức tập 2
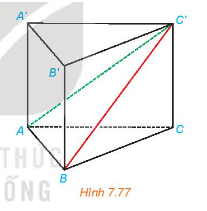
Cho hình lăng trụ đứng ABC.A'B'C' có ABC là tam giác vuông cân tại A, AB=a, AA'= h (H.7.77).
a) Tinh khoảng cách từ A đến mặt phẳng (BCC'B').
b) Tam giác ABC' là tam giác gì? Tính khoảng R cách từ A đến BC'.
Hướng dẫn giải chi tiết Luyện tập 1
Phương pháp giải
HS xem lại lý thuyết các bài đã học để trả lời câu hỏi này nhé.
Lời giải chi tiết
a) Gọi E là trung điểm của CC'. Khoảng cách từ A đến mặt phẳng (BCC'B') chính là khoảng cách từ A đến đoạn thẳng BE.
Ta có nên
Ta biết rằng vuông góc với và do . Từ đó, ta suy ra :
Mặt khác, ta có thể
do đó
Khoảng cách từ là:
b) Ta có Vì nên \( BB'. BC'=0 \( Mặt khác ta có:
Do đó:
Vậy tam giác ABC' là tam giác vuông cân tại C'.
Khoảng cách từ A đến BC' là:
-- Mod Toán 11 HỌC247
Chưa có câu hỏi nào. Em hãy trở thành người đầu tiên đặt câu hỏi.
Bài tập SGK khác
Hoạt động 1 trang 54 SGK Toán 11 Kết nối tri thức tập 2 - KNTT
Hoạt động 2 trang 55 SGK Toán 11 Kết nối tri thức tập 2 - KNTT
Hoạt động 3 trang 56 SGK Toán 11 Kết nối tri thức tập 2 - KNTT
Luyện tập 2 trang 56 SGK Toán 11 Kết nối tri thức tập 2 - KNTT
Vận dụng trang 57 SGK Toán 11 Kết nối tri thức tập 2 - KNTT
Hoạt động 4 trang 57 SGK Toán 11 Kết nối tri thức tập 2 - KNTT
Khám phá trang 58 SGK Toán 11 Kết nối tri thức tập 2 - KNTT
Giải Bài 7.22 trang 59 SGK Toán 11 Kết nối tri thức tập 2 - KNTT
Giải Bài 7.23 trang 59 SGK Toán 11 Kết nối tri thức tập 2 - KNTT
Giải Bài 7.24 trang 59 SGK Toán 11 Kết nối tri thức tập 2 - KNTT
Giải Bài 7.25 trang 59 SGK Toán 11 Kết nối tri thức tập 2 - KNTT
Giải Bài 7.26 trang 59 SGK Toán 11 Kết nối tri thức tập 2 - KNTT
Giải Bài 7.27 trang 59 SGK Toán 11 Kết nối tri thức tập 2 - KNTT
Bài tập 7.27 trang 37 SBT Toán 11 Tập 2 Kết nối tri thức - KNTT
Bài tập 7.28 trang 38 SBT Toán 11 Tập 2 Kết nối tri thức - KNTT
Bài tập 7.29 trang 38 SBT Toán 11 Tập 2 Kết nối tri thức - KNTT
Bài tập 7.30 trang 38 SBT Toán 11 Tập 2 Kết nối tri thức - KNTT
Bài tập 7.31 trang 38 SBT Toán 11 Tập 2 Kết nối tri thức - KNTT
Bài tập 7.32 trang 38 SBT Toán 11 Tập 2 Kết nối tri thức - KNTT