Giải bài 86 tr 172 SBTToán lớp 9 Tập 1
Cho đường tròn \((O),\) đường kính \(AB,\) điểm \(C\) nằm giữa \(A\) và \(O.\) Vẽ đường tròn \((O')\) có đường kính \(CB.\)
\(a)\) Hai đường tròn \((O)\) và \((O')\) có vị trí tương đối như thế nào đối với nhau \(?\)
\(b)\) Kẻ dây \(DE\) của đường tròn \((O)\) vuông góc với \(AC\) tại trung điểm \(H\) của \(AC.\) Tứ giác \(ADCE\) là hình gì \(?\) Vì sao\(?\)
\(c)\) Gọi \(K\) là giao điểm của \(DB\) và đường tròn \((O').\) Chứng minh rằng ba điểm \(E, C, K\) thẳng hàng.
\(d)\) Chứng minh rằng \(HK\) là tiếp tuyến của đường tròn \((O').\)
Hướng dẫn giải chi tiết
Hướng dẫn giải
Sử dụng kiến thức:
+) Nếu \(OO' = R – r\) thì đường tròn \((O)\) và đường tròn \((O')\) tiếp xúc trong.
+) Trong một đường tròn, đường kính vuông góc với một dây thì đi qua trung điểm của dây ấy.
+) Tứ giác có hai đường chéo cắt nhau tại trung điểm mỗi đường là hình bình hành.
+) Hình bình hành có hai đường chéo vuông góc là hình thoi.
+) Để chứng minh ba điểm thẳng hàng, ta chứng minh ba điểm xác định được hai đường thẳng cùng vuông góc với một đường thẳng thứ ba.
+) Trong tam giác vuông, đường trung tuyến ứng với cạnh huyền bằng nửa cạnh huyền.
+) Nếu một đường thẳng đi qua một điểm của đường tròn và vuông góc với bán kính đi qua điểm đó thì đường thẳng ấy là một tiếp tuyến của đường tròn.
Lời giải chi tiết
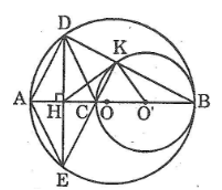
\(a)\) Vì \(O, O'\) và \(B\) thẳng hàng nên: \(O'B < OB\)\( ⇒ O'\) nằm giữa \(O\) và \(B\)
Ta có: \(OO' = OB - O'B\)
Vậy đường tròn \((O')\) tiếp xúc trong với đường tròn \((O)\) tại \(B.\)
\(b)\) Xét đường tròn (O) có \(AB ⊥ DE\;\; (gt)\) mà AB là đường kính, DE là dây cung
Suy ra: \(HD = HE\) (đường kính vuông góc với dây cung)
Lại có: \(HA = HC \;\;(gt)\)
Suy ra, tứ giác \(ADCE\) có hai đường chéo cắt nhau tại trung điểm của mỗi đường nên nó là hình bình hành.
Lại có: \(AC ⊥ DE\)
Suy ra tứ giác \(ADCE\) là hình thoi.
\(c)\) Tam giác \(ABD\) nội tiếp trong đường tròn \((O)\) có \(AB\) là đường kính nên vuông tại \(D.\)
Suy ra: \(AD ⊥ BD\)
Tứ giác \(ADCE\) là hình thoi nên \(EC // AD\)
Suy ra: \( EC ⊥ BD \;\;\; (1)\)
Tam giác \(BCK\) nội tiếp trong đường tròn \((O')\) có \(BC\) là đường kính nên vuông tại \(K.\)
Suy ra: \(CK ⊥ BD\;\;\; (2)\)
Từ \((1)\) và \((2)\) suy ra \(EC\) trùng với \(CK\)
Vậy \(E, C, K\) thẳng hàng.
\(d)\) Tam giác \(DEK\) vuông tại \(K\) có \(KH\) là trung tuyến ứng với cạnh huyền \(DE\) nên:
\(HK = HE = \displaystyle{1 \over 2}DE\) (tính chất tam giác vuông)
Suy ra tam giác \(EHK\) cân tại \(H\)
Suy ra: \(\widehat {HEK} = \widehat {HKE}\) (tính chất tam giác cân) \((3)\)
Ta có: \(O'K = O'C \) (= bán kính đường tròn (O')) nên tam giác \(O'CK\) cân tại \(O'\)
Suy ra: \(\widehat {O'KC} = \widehat {O'CK}\) (tính chất tam giác cân)
Mà: \(\widehat {O'CK} = \widehat {HCE}\) (đối đỉnh)
Suy ra: \(\widehat {O'KC} = \widehat {HCE}\) \( (4)\)
Từ \((3)\) và \((4)\) suy ra: \(\widehat {HKO'} = \widehat {HKE} + \widehat {O'KC}\)\( = \widehat {HEK} + \widehat {HCE}\) \((5)\)
Tam giác \(CEH\) vuông tại \(H\) nên \(\widehat {HEK} + \widehat {HCE} = 90^\circ \) \((6)\)
Từ \((5)\) và \((6)\) suy ra: \(\widehat {HKO'} = 90^\circ \) hay \(HK ⊥ KO'\) tại \(K\)
Vậy \(HK\) là tiếp tuyến của đường tròn \((O').\)
-- Mod Toán 9 HỌC247
-


Chứng minh góc BEI = góc CFI
bởi Lê Nhật Minh
 26/01/2019
26/01/2019
Cho tam giác ABC có AB < AC. Trên cạnh AB và CA lần lượt lấy M và N di động sao cho BM = CN. Gọi I và G theo thứ tự là trung điểm của DC và MN. Đường thẳng IG cắt các đường thẳng AB và AC tại E và F. Chứng munh góc BEI = góc CFI
Theo dõi (0) 1 Trả lời -


rút gọn biểu thức:
\(\sin^235^o+\tan22^o-\frac{\cot13^o}{\tan77^o}-\cot68^o+\sin^255^o\)
làm gấp giúp mình nha
Theo dõi (0) 1 Trả lời -


Chứng minh rằng k phụ thuộc vào α
A=4sin^4α.cos2α+(sin2α-cos2α)2+4cos^4α.sin2α
Theo dõi (0) 1 Trả lời -


Trên quả đồi có 1 cái tháp cao 100m. Từ đỉnh B và chân của tháp nhìn lên điểm A ở dưới chân đồi dưới các góc tương ứng 60 độ và 30 độ . Hãy tính chiều cao H của quả đồi
Theo dõi (0) 1 Trả lời -


Đơn giản biểu thức (1-cosx)(1+cosx) - sin^2x
bởi can tu
 26/01/2019
26/01/2019
Đơn giản biểu thức: a) (1-cosx)(1+cosx) - sin^2x
b) tg^2x (2cos^2x + sin^2x - 1) + cos^2x
Theo dõi (0) 1 Trả lời -


Chứng minh AM.AB=AN.AC
bởi Trần Hoàng Mai
 26/01/2019
26/01/2019
cho \(\Delta ABC\) nhọn,đường cao AH. Gọi M,N lần lượt là hình chiếu của H trên AB,AC.
a) Chứng minh AM.AB=AN.AC
b) chứng minh \(AH=\dfrac{BC}{cotB+cotC}\)
c) cho \(BC=MN\sqrt{2}\). Chứng minh \(S_{\Delta AMN}=S_{\Delta BMNC}\)
Theo dõi (0) 1 Trả lời -


Tính tỉ số HB và HC có BD=36cm và CD=60cm
bởi Lê Gia Bảo
 26/01/2019
26/01/2019
Cho tam giác ABC vuông tại A. Đường phân giác AD chia cạnh BC thành hai đoạn BD=36cm và CD=60cm. kẻ đường cao AH (H€BC)
a) Tính tỉ số HB và HC
b) tính AH.
Theo dõi (0) 1 Trả lời -


Chứng minh Δ ABC vuông và tính độ dài AH
bởi Phạm Phú Lộc Nữ
 26/01/2019
26/01/2019
cho tam giác ABC có AB = 6cm, AC = 8cm, BC =10cm. kẻ\(AH\perp BC\); \(HK\perp AC\) ( H\(\in\)BC; K\(\in\)AC)
a) Chứng minh \(\Delta\)ABC vuông và tính độ dài AH
b) Tính AK
c) Gọi góc BKH =\(\alpha\). Tính các tỉ số lượng của góc \(\alpha\)
Theo dõi (0) 1 Trả lời





