Bài tập 85 trang 172 SBT Toán 9 Tập 1

Hướng dẫn giải

Sử dụng kiến thức:

+) Tam giác nội tiếp đường tròn, có một cạnh là đường kính thì tam giác đó là tam giác vuông.

+) Trong tam giác, ba đường cao cắt nhau tại một điểm gọi là trực tâm tam giác.

+)  Hai điểm gọi là đối xứng với nhau qua \(O\) nếu \(O\) là trung điểm của đoạn thẳng nối hai điểm đó.

+) Tứ giác có hai đường chéo cắt nhau tại trung điểm mỗi đường là hình bình hành.

+) Nếu một đường thẳng đi qua một điểm của đường tròn và vuông góc với bán kính đi qua điểm đó thì đường thẳng ấy là một tiếp tuyến của đường tròn.

Lời giải chi tiết

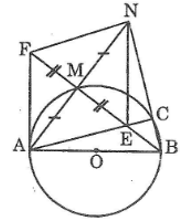
\(a)\) Tam giác \(ABM\) nội tiếp trong đường tròn \((O)\) có \(AB\) là đường kính nên vuông tại \(M\)

Suy ra: \(AN ⊥ BM\)

Tam giác \(ABC\) nội tiếp trong đường tròn \((O)\) có \(AB\) là đường kính nên vuông tại \(C\)

Suy ra: \(AC ⊥ BN\)

Tam giác \(ABN\) có hai đường cao \(AC\) và \(BM\) cắt nhau tại \(E\) nên \(E\) là trực tâm của tam giác \(ABN\) 

Suy ra: \(NE ⊥ AB\)

\(b)\) Ta có: \(MA = MN\) ( tính chất đối xứng tâm)

                 \(ME = MF\) ( tính chất đối xứng tâm)

Tứ giác \(AENF\) có hai đường chéo cắt nhau tại trung điểm của mỗi điểm đường nên nó là hình bình hành.

Suy ra:    \(AF // NE\)

Mà          \(NE ⊥ AB\) ( chứng minh trên)

Suy ra: \(AF ⊥ AB\) tại \(A.\)

Vậy \(FA\) là tiếp tuyến của đường tròn \((O).\)

\(c)\) Trong tam giác \(ABN\) ta có: \(AN ⊥ BM\) và \(AM = MN\) hay BM vừa là đường cao vừa là đường trung tuyến nên tam giác \(ABN\) cân tại \(B.\)

Suy ra \(BA = BN\) hay \(N\) thuộc đường tròn \((B; BA)\)

Tứ giác \(AFNE\) là hình bình hành nên  \(AE // FN\) hay \(FN // AC\)

Mặt khác: \(AC ⊥ BN\) ( chứng minh trên)

Suy ra: \(FN ⊥ BN \) tại \(N\)

Vậy \(FN\) là tiếp tuyến của đường tròn \(( B; BA).\)

-- Mod Toán 9 HỌC247