Giải bài 84 tr 171 SBTToán lớp 9 Tập 1
Cho tam giác ABC vuông tại A (AB < AC) nội tiếp trong đường tròn (O) có đường kính BC. Kẻ dây AD vuông góc với BC. Gọi E là giao điểm của DB và CA. Qua E kẻ đường thẳng vuông góc với BC, cắt BC ở H, cắt AB ở F. Chứng minh rằng:
a. Tam giác EBF cân
b. Tamm giác HAF cân
c. HA là tiếp tuyến của đường tròn (O)
Hướng dẫn giải chi tiết
Hướng dẫn giải
Sử dụng kiến thức:
+) Sử dụng tính chất đường trung trực: Điểm nằm trên đường trung trực của một đoạn thẳng thì cách đều hai đầu mút của đoạn thẳng đó.
+) Trong tam giác cân, đường cao ứng với cạnh đáy cũng là đường phân giác, trung tuyến, trung trực.
+) Trong tam giác vuông, đường trung tuyến ứng với cạnh huyền bằng nửa cạnh huyền.
+) Nếu một đường thẳng đi qua một điểm của đường tròn và vuông góc với bán kính đi qua điểm đó thì đường thẳng ấy là một tiếp tuyến của đường tròn.
Lời giải chi tiết
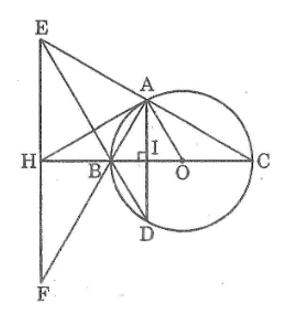
\(a)\) Gọi \(I\) là giao điểm của \(AD\) và \(BC\).
Xét đường tròn (O) có đường kính \(BC\bot AD\) tại I nên I là trung điểm của dây AD (định lý)
Suy ra \(BC\) là đường trung trực của \(AD\) nên theo tính chất đường trung trực ta có: \( BA = BD\)
Tam giác \(BAD\) cân tại \(B\) có \(BI ⊥ AD\) nên \(BI\) là tia phân giác của góc \(ABD.\)
Suy ra: \(\widehat {ABI} = \widehat {DBI}\)
Mà \(\widehat {ABI} = \widehat {HBF}\) (đối đỉnh)
và \(\widehat {DBI} = \widehat {HBE}\) ( đối đỉnh)
Suy ra: \(\widehat {HBE} = \widehat {HBF}\)
Do đó \(BH\) là tia phân giác của góc \(EBF\)
Tam giác \(EBF\) có \(BH\) là tia phân giác của góc \(EBF\) và \(BH ⊥ EF\) nên tam giác \(EBF\) cân tại \(B.\)
\(b)\) Tam giác \(EBF\) cân tại \(B\) có BH là đường cao nên BH cũng là đường trung tuyến.
Suy ra \(HE = HF\)
Tam giác \(AEF\) vuông tại \(A\) có \(AH\) là đường trung tuyến ứng với cạnh huyền nên:
\(HA = HE = HF = \displaystyle {1 \over 2}{\rm{EF}}\) (tính chất tam giác vuông)
Vậy tam giác \(AHF\) cân tại \(H.\)
\(c)\) Tam giác \(AHF\) cân tại \(H\) nên \(\widehat {HAF} = \widehat {HFA}\) \((1)\)
Tam giác \(AOB\) cân tại \(O\) nên \(\widehat {OAB} = \widehat {OBA}\)
Mà \(\widehat {ABI} = \widehat {HBF}\) ( đối đỉnh)
Suy ra: \(\widehat {OAB} = \widehat {HBF}\) \((2)\)
Từ \((1)\) và \((2)\) suy ra: \(\widehat {HAO} = \widehat {{\rm{HAF}}} + \widehat {OAB}\)\( = \widehat {HFB} + \widehat {HBF}\) \((3)\)
Tam giác \(BHF\) vuông tại \(H\) nên \(\widehat {HFB} + \widehat {HBF} = 90^\circ \) \( (4)\)
Từ \((3)\) và \((4)\) suy ra: \(\widehat {HAO} = 90^\circ \) hay \(HA ⊥ AO\)
Vậy \(HA\) là tiếp tuyến của đường tròn \((O).\)
-- Mod Toán 9 HỌC247
-


Chứng minh Δ MND vuông tại M
bởi Hy Vũ
 24/01/2019
24/01/2019
Cho Δ MND có MN=10 cm, MD = 24cm DN= 26
a) Chứng minh Δ MND vuông tại M
b) Tính đường cao MI , góc N ,D
c) Vẽ IH vuông góc với MD, IK vuông góc với MN . Chứng minh : HK=MI
d) Từ M kẻ đường trung tuyến MQ, Q thuộc ND . Tính góc IMQ
Theo dõi (0) 1 Trả lời -


Chứng minh góc BAH =MAC
bởi Hy Vũ
 24/01/2019
24/01/2019
Cho tam giác ABC có góc A bằng 90 độ, kẻ đường cao AH và trung tuyến AM kẻ HD vuông góc AB, HE vuông góc AC, biết HB=4,5cm; HC=8cm.
a, CM: góc BAH =MAC
b, CM: AM vuông góc DE tại K
c, Tính độ dài AK
chủ yếu là câu b với câu c nha!!!
Theo dõi (0) 1 Trả lời -


Chứng minh rằng BE^2 = BH^3/ BC
bởi Mai Trang
 24/01/2019
24/01/2019
cho ΔABC có góc A vuông và đường cao AH gọi HE,HF lẩn lượt là các dường cao của ΔAHB và ΔAHC
A, CMR, \(BE^2\)= \(\dfrac{BH^3}{BC}\)
B, biết BC=2a tính a theo giá trị\(\sqrt[3]{BE^2}\)+\(\sqrt[3]{CF^2}\)
Theo dõi (0) 1 Trả lời -


Tính B, biết độ dà AB = 6 c m, AC = 8cm
bởi Lê Nguyễn Hạ Anh
 24/01/2019
24/01/2019
Cho \(\Delta\)ABC vuông tại A, đường cao AH (H \(\in\) BC).Từ H kẻ HE\(\perp\)AB tại E, \(HF\perp AC\) tại F. Biết độ dà AB\(=6cm\),AC\(=\)8cm
a, Tính \(\sin\)B, \(\cos B\)
b, Tính EF
c, Chứng minh \(AB\times AE=AC\times AF\)
Giúp mk vs mk lm đk câu a và câu b, câu c bn nào biết thì giúp mk vs mk đang cần gấp
 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


Tính độ dài cạnh AC đường cao AH, biết AB =6 cm, BH=3cm
bởi Lan Anh
 24/01/2019
24/01/2019
Câu 1 Cho tam giác ABC vuông tại A đường cao AH biết AB =6 cm, BH=3cm . Hãy tính độ dài cạnh AC đường cao AH
Câu 2 Cho tam giác OPQ vuông tai O đường cao OH biết OP= 6cm. PH = 3cm. Tính độ dài cạnh OQ. Đường cao OH
Giúp mình với các bạn ơi . Mai mình kiểm tra rồi. Cảm ơn
Theo dõi (0) 1 Trả lời -


Chứng minh rằng góc DEC=90^0
bởi Choco Choco
 24/01/2019
24/01/2019
Cho tam giác ABC vuông tại A, đường cao AH. Gọi D là điểm đối xứng với A qua B. Gọi E là điểm thuộc tia đối của tia HA sao cho HE = 2HA. CMR: \(\widehat{DEC=90^o}\)
Theo dõi (0) 1 Trả lời -


Tính thời gian từ lúc 2 kim đồng hồ gặp nhau lần trước đến lúc chúng gặp nhau lần tiếp theo
bởi Dell dell
 28/02/2019
28/02/2019
Bài 1:
a) Tính thời gian từ lúc 2 kim đồng hồ gặp nhau lần trước đến lúc chúng gặp nhau lần tiếp theo
b) Trong 1 ngày, 2 kim đồng hồ tạo với nhau góc vuông bao nhiêu lần
Theo dõi (0) 2 Trả lời -


Tính độ dài BC, có AB= 10cm, góc ABC= 40 độ
bởi hi hi
 25/01/2019
25/01/2019
cho tam giác abc vuông tại a có ab= 10cm, góc abc= 40 độ
a, tính độ dài bc
b, kẻ tia phân giác bd của góc abc ( d thuộc ac). tính ad
Theo dõi (0) 1 Trả lời
Bài tập SGK khác
Bài tập 82 trang 171 SBT Toán 9 Tập 1
Bài tập 83 trang 171 SBT Toán 9 Tập 1
Bài tập 85 trang 172 SBT Toán 9 Tập 1
Bài tập 86 trang 172 SBT Toán 9 Tập 1
Bài tập 87 trang 172 SBT Toán 9 Tập 1
Bài tập 88 trang 172 SBT Toán 9 Tập 1
Bài tập 88 trang 172 SBT Toán 9 Tập 1
Bài tập II.1 trang 173 SBT Toán 9 Tập 1





