Bài tập 87 trang 172 SBT Toán 9 Tập 1

Hướng dẫn giải

Sử dụng kiến thức: 

+) Nếu hai đường tròn tiếp xúc nhau thì tiếp điểm nằm trên đường nối tâm.

+) Trong một đường tròn, đường kính vuông góc với một dây thì đi qua trung điểm của dây ấy.

+) Tứ giác có hai đường chéo cắt nhau tại trung điểm mỗi đường là hình bình hành.

+) Hình bình hành có hai đường chéo vuông góc là hình thoi.

+) Để chứng minh ba điểm thẳng hàng, ta chứng minh ba điểm xác định được hai đường thẳng cùng vuông góc với một đường thẳng thứ ba.

+) Trong tam giác vuông, đường trung tuyến ứng với cạnh huyền bằng nửa cạnh huyền.

+) Nếu một đường thẳng đi qua một điểm của đường tròn và vuông góc với bán kính đi qua điểm đó thì đường thẳng ấy là một tiếp tuyến của đường tròn.

Lời giải chi tiết

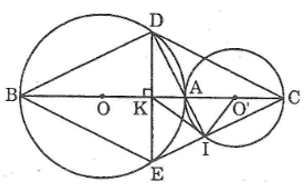
\(a)\) Vì đường tròn \((O)\) và \((O')\) tiếp xúc ngoài tại \(A\) nên \(O, A\) và \(O'\) thẳng hàng.

Trong đường tròn \((O)\) ta có: \( AB ⊥ DE\) tại \(K\) mà AB là đường kính và DE là dây cung

Suy ra: \(KD = KE\) ( đường kính vuông góc với dây cung)

Lại có: \(KB = KC (gt)\)

Suy ra tứ giác \(BDCE\) có hai đường chéo cắt nhau tại trung điểm của mỗi đường nên nó là hình bình hành.

Lại có: \(BC ⊥ DE\)

Suy ra tứ giác \(BDCE\) là hình thoi.

\(b)\) Tam giác \(ABD\) nội tiếp trong đường tròn \((O)\) có \(AB\) là đường kính nên vuông tại \(D.\)

Suy ra: \(AD ⊥ BD\)

Tứ giác \(BDCE\) là hình thoi nên \(EC // BD\)

Suy ra: \(EC ⊥ AD\;\;  (1)\)

Tam giác \(AIC\) nội tiếp trong đường tròn \((O')\) có \(AC\) là đường kính nên vuông tại \(I.\)

Suy ra: \(AI ⊥ CE\;\;(2)\)

Từ \((1)\) và \((2)\) suy ra \(AD\) trùng với \(AI\)

Vậy \(D, A, I\) thẳng hàng.

c) Tam giác \(DIE\) vuông tại \(I\) có \(IK\) là trung tuyến ứng với cạnh huyền \(DE\) nên:

\(KI = KD = \displaystyle {1 \over 2}ED\) ( tính chất tam giác vuông)

Suy ra tam giác \(IKD\) cân tại \(K\)

Suy ra: \(\widehat {KID} = \widehat {KDI}\) hay \(\widehat {KIA} = \widehat {KDA}\)   \((3)\)

Ta có: \(O'A = O'I \) (= bán kính đường tròn (O')) nên tam giác \(O'IA\) cân tại \(O'\)

Suy ra: \(\widehat {O'AI} = \widehat {O'IA}\) ( tính chất tam giác cân)

Mà: \(\widehat {O'AI} = \widehat {KAD}\) (đối đỉnh)

Suy ra: \(\widehat {O'IA} = \widehat {KAD}\)  \( (4)\)

Từ \((3)\) và \((4)\) suy ra: \(\widehat {KIO'}=\widehat {KIA}+\widehat {AIO'}\)\(=\widehat {KDA}+\widehat {KAD}\)

Xét tam giác KAD vuông tại K có: \(\widehat {KDA}+\widehat {KAD}=90^0\)

Suy ra \(\widehat {KIO'} = 90^\circ \) hay \(KI ⊥ O'I\) tại \(I.\)

Vậy \(KI\) là tiếp tuyến của đường tròn \((O').\)

-- Mod Toán 9 HỌC247