Bài tập 7.1 tr 107 sách BT Toán lớp 9 Tập 2
Cho tam giác \(ABC\) có ba góc nhọn. Vẽ các đường cao \(AI, BK, CL\) của tam giác ấy.Gọi \(H\) là giao điểm của các đường cao vừa vẽ.
\(a)\) Chỉ ra các tứ giác nội tiếp có đỉnh lấy trong số các điểm \(A, B, C, H, I, K, L\)
\(b)\) Chứng minh \(\widehat {LBH},\widehat {LIH},\widehat {KIH}\) và \(\widehat {KCH}\) là \(4\) góc bằng nhau.
\(c)\) Chứng minh \(KB\) là tia phân giác của \(\widehat {LKI}.\)
Hướng dẫn giải chi tiết
Hướng dẫn giải
Ta sử dụng kiến thức:
+) Nếu một tứ giác có tổng số đo hai góc đối nhau bằng \(180^\circ\) thì tứ giác đó nội tiếp được đường tròn.
+) Tứ giác có hai đỉnh cùng nhìn một cạnh dưới một góc vuông là tứ giác nội tiếp.
+) Trong một đường tròn, các góc nội tiếp cùng chắn một cung thì bằng nhau.
Lời giải chi tiết
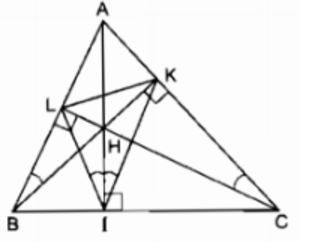
Vì \(∆ABC\) là tam giác nhọn nên ba đường cao cắt nhau tại điểm \(H\) nằm trong tam giác \(ABC.\)
\(a)\) Tứ giác \(AKHL\) có: \(\widehat {AKH} + \widehat {ALH} = 90^\circ + 90^\circ = 180^\circ \)
Nên tứ giác \(AKHL\) nội tiếp.
\(+)\) Tứ giác \(BIHL\) có: \(\widehat {BIH} + \widehat {BLH} = 90^\circ + 90^\circ = 180^\circ \)
Nên tứ giác \(BIHL\) nội tiếp.
\(+)\) Tứ giác \(CIHK\) có: \(\widehat {CIH} + \widehat {CKH} = 90^\circ + 90^\circ = 180^\circ \)
Nên tứ giác \(CIHK\) nội tiếp.
\(+)\) Tứ giác \(ABIK\) có: \(\widehat {AKB} = 90^\circ;\widehat {AIB} = 90^\circ \)
\(K\) và \(I\) nhìn đoạn \(AB\) dưới một góc vuông nên tứ giác \(ABIK\) nội tiếp.
\(+)\) Tứ giác \(BCKL\) có \(\widehat {BKC} = 90^\circ;\widehat {BLC} = 90^\circ \)
Suy ra\(K\) và \(L\) nhìn đoạn \(BC\) dưới một góc vuông nên tứ giác \(BCKL\) nội tiếp.
\(+)\) Tứ giác \(ACIL\) có \(\widehat {AIC} = 90^\circ;\widehat {ALC} = 90^\circ \)
Suy ra\(I\) và \(L\) nhìn đoạn \(AC\) dưới một góc vuông nên tứ giác \(ACIL\) nội tiếp.
\(b)\) Tứ giác \(BIHL\) nội tiếp.
\( \Rightarrow \widehat {LBH} = \widehat {LIH}\) \((\)\(2\) góc nội tiếp cùng chắn cung nhỏ \(\overparen{LH}\)\()\) \( \;\;(1)\)
Tứ giác \(CIHK\) nội tiếp.
\( \Rightarrow \widehat {HIK} = \widehat {HCK}\) \((2\) góc nội tiếp cùng chắn cung nhỏ \(\overparen{HK}\)\()\) \(\;\;(2)\)
Tứ giác \(BCKL\) nội tiếp.
\( \Rightarrow \widehat {LBK} = \widehat {LCK}\) \((2\) góc nội tiếp cùng chắn cung nhỏ \(\overparen{LK}\)) hay \(\widehat {LBH} = \widehat {HCK}\) \( \;\;(3)\)
Từ \((1),\) \((2)\) và \((3)\) suy ra \(\widehat {LBH}=\widehat {LIH}=\widehat {KIH}\)\(=\widehat {KCH}\)
c) Tứ giác \(CIHK\) nội tiếp.
\( \Rightarrow \widehat {ICH} = \widehat {IKH}\) \((\)\(2\) góc nội tiếp cùng chắn cung nhỏ \(\overparen{IH}\)\()\) \( \;\;(*)\)
Tứ giác \(LKCB\) nội tiếp.
\( \Rightarrow \widehat {LCB} = \widehat {LKB}\) \((\)\(2\) góc nội tiếp cùng chắn cung nhỏ \(\overparen{LB}\)\()\) \( \;\;(**)\)
Từ (*) và (**) suy ra \(\widehat {LKH} = \widehat {HKI}\). Vậy \(KB\) là tia phân giác của \(\widehat {LKI}.\)
-- Mod Toán 9 HỌC247
-


Bài 39 trang 106 sách bài tập toán 9 tập 2
bởi Lê Tấn Vũ
 08/10/2018
08/10/2018
Bài 39 (Sách bài tập - tập 2 - trang 106)
Trên đường tròn tâm O có một cung AB và S là điểm chính giữa của cung đó. Trên dây AB lấy hai điểm E và H. Các đường thẳng SH và SE cắt đường tròn theo thứ tự tại C và D. Chứng minh EHCD là một tứ giác nội tiếp ?
Theo dõi (0) 2 Trả lời -


Cho đường tròn tâm O. Từ A là một điểm nằm ngoài (O) kẻ các tiếp tuyến AM, AN với (O) (M;N là các tiếp điểm)
1, Chứng minh rằng tứ giác AMON nội tiếp đường tròn đường kính AO
2, Đường thẳng qua A cắt đường tròn (O) tại B và C ( B nằm giữa A và C). Gọi I là trung điểm của BC. Chứng minh I cũng thuộc đường tròn đường kính AO.
3, Gọi K là giao điểm của MN và BC. Chứng minh rằng AK.AI=AB.AC
Theo dõi (0) 1 Trả lời -


Chứng minh rằng tứ giác BDEC nội tiếp đường tròn
bởi Nguyễn Thị Lưu
 22/02/2019
22/02/2019
Cho nửa đường tròn đường kính BC =2R. Từ điểm A trên nửa đường tròn vẽ AH vuông góc BC. Nửa đường tròn đường kính BH, CH lần lượt có tâm O1; O2 cắt AB, AC thứ tự tại D và E
Chứng minh rằng : tứ giác BDEC nội tiếp đường tròn
Theo dõi (0) 1 Trả lời -


Chứng minh BDIM nội tiếp, BIJC là hình bình hành
bởi thu trang
 22/10/2018
22/10/2018
cho tam giác ABC có 3 cạnh góc nhọn trung tuyến AM có độ dài bằng cạnh BC. Đường tròn đường kính BC cắt các cạnh AB,AC theo thứ tự D và E. đường tròn ngoại tiếp tam giác ADE và đường tròn ngoại tiếp tam giác ABC cắt AM lần lượt tịa I và J.chứng minh BDIM nội tiếp, BIJC là hình bình hành
Theo dõi (0) 1 Trả lời -


Chứng minh OM=1/2AH biết tam giác ABC nhọn nội tiếp đường O bán kính R
bởi Nguyễn Hoàng Phú
 17/08/2018
17/08/2018
Cho tâm giác ABC nhọn nội tiếp đường O bán kính R, trực tâm H. kê đường vuông góc OM vuông góc với BC chứng minh. a, OM = 1/2AH b,AH^2 +BC^2 = 4R^2 Có thể phần b sai đề nhá nhưng làm phần a thôi có dc
Theo dõi (1) 0 Trả lời -


Chứng minh (AB/CD)+(CD/AB)+(BC/AD)+(AD/BC) < = (IA/IC)+(IC/IA)+(IB/ID)+(ID/IB)
bởi Nguyễn Minh Hiếu
 25/05/2018
25/05/2018
Bài 1: Cho tứ giác ABCD nội tiếp đường tròn (O) có I là giao điểm của AC và BD. Chứng minh:
(AB/CD)+(CD/AB)+(BC/AD)+(AD/BC) ≤ (IA/IC)+(IC/IA)+(IB/ID)+(ID/IB)
Bài 2: Cho tam giác ABC nội tiếp đường tròn (O; R). Gọi I là điểm bất kỳ nằm trong tam giác ABC ( I không nằm trên cạnh của tam giác). Các tia AI; BI; CI lần lượt cắt BC; CA; AB tại M; N; P.
a) Chứng minh: (AI/AM) + (BI/BM) + (CI/CM) = 2
b) Chứng minh: (1/AM.BN) + (1/BN.CP) + (1/CP.AM) ≤ (4/(3(R−OI)2))Theo dõi (0) 1 Trả lời -


Chứng minh 3 điểm H,E,I thẳng hàng biết tam giác ABC có 3 góc nhọn và nội tiếp trong (O)
bởi Phạm Thị Lương Minh
 18/05/2018
18/05/2018
Tam giác ABC có 3 góc nhọn và nội tiếp trong (O). Hai đường cao AD,BK cắt nhau tại H. Kéo dài BK cắt (O) tại F, vẽ đường kính BE của (O) và gọi I là trung điểm của AC. Chứng minh 3 điểm H,E,I thẳng hàng
Theo dõi (0) 1 Trả lời -


Cho đường tròn (O;3cm), từ một điểm A nằm ngoài đường tròn vẽ hai tiếp tuyến AB, AC (B;C là các tiếp điểm)
a. Chứng minh tứ giác ABOC nội tiếp được đường tròn
b. Đường thẳng AO cắt đường tròn tại M, N (M nằm giữa A và N)
Chứng minh AB2=AM.AN
c. Cho ^BAO = 30° hãy tính diện tích hình viên phân giới hạn bởi dây BM và cung nhỏ BM
Theo dõi (0) 3 Trả lời -


Chứng minh 4 điểm A, C, D, E cùng thuộc 1 đường tròn biết C là điểm bất kì trên cung AB nhỏ
bởi Ngát Hồng
 27/04/2018
27/04/2018
Cho điểm M cố định nằm ngoài đường tròn (O;R). Qua M vẽ các tiếp tuyến MA, MB với đường tròn O. Gọi C là điểm bất kì trên cung AB nhỏ. Gọi D,E,F lần lượt là chân đường vuông góc kẻ từ C đến AB, MA, MB.
a) Chứng minh: 4 điểm A,C,D,E cùng thuộc 1 đtron
b)AC cắt DE tại P, BC cắt DF tại Q. Chứng minh tam giác PAE đồng dạng với tam giác PDC
c) chứng minh PQ//AB
Theo dõi (1) 0 Trả lời -


Chứng minh N là trung điểm của IK biết qua N vẽ đường thẳng vuông góc với CE
bởi Nhi Quỳnh
 18/04/2018
18/04/2018
Cho tam giác nhọn ABC (AB < AC). Đường tròn (O) đường kính BC cắt AB và AC lần lượt tại E và D. Gọi H là giao điểm của BD và CE. Tia AH cắt BC tại F.
- Chứng minh: HB.HD = HC.HE và AF vuông góc BC.
- Gọi M là trung điểm của CH. Chứng minh tứ giác OMEF là tứ giác nội tiếp.
- DF cắt CE tại N. Qua N vẽ đường thẳng vuông góc với CE cắt BC và BD lần lượt tại I và K. Chứng minh N là trung điểm của IK.
Theo dõi (2) 1 Trả lời -


Cho đường tròn (O; R) có đường kính AB = 2R. Trên tiếp tuyến Ax lấy điểm M sao cho OM > 2R. Kẻ dây AC của (O) vuông góc với OM tại H, MB cắt đường tròn (O) và AC lần lượt tại D và T.
- Chứng minh: MC là tiếp tuyến và tứ giác MAOC nội tiếp đường tròn. Xác định tâm I của đường tròn.
- Đường tròn (I) cắt MB tại E (E khác M). Chứng minh OE // AD.
- Chứng minh TD.TB = TM.TE.
Theo dõi (1) 1 Trả lời





