Bài tập 42 tr 107 sách BT Toán lớp 9 Tập 2
Cho ba đường tròn cùng đi qua một điểm \(P.\) Gọi các giao điểm khác \(P\) của hai trong ba đường tròn đó là \(A, B, C.\) Từ một điểm \(D\) (khác điểm \(P\)) trên đường tròn \((PBC)\) kẻ các tia \(DB, DC\) cắt các đường tròn \((PAB)\) và \((PAC)\) lần lượt tại \(M, N.\) Chứng minh ba điểm \(M, A, N\) thẳng hàng.
Hướng dẫn giải chi tiết
Hướng dẫn giải
Ta sử dụng kiến thức:
+) Trong một tứ giác nội tiếp, tổng số đo hai góc đối nhau bằng \(180^\circ.\)
+) Chứng minh ba điểm thẳng hàng: Nếu \( \widehat{ABD}+\widehat{DBC}=180^\circ\) thì \(A,B,C\) thẳng hàng.
Lời giải chi tiết
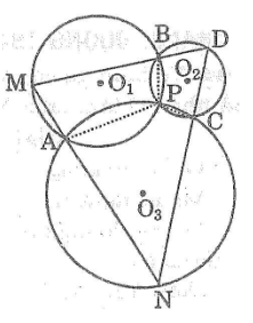
Gọi ba đường tròn tâm \(O_1,O_2,O_3.\)
\((O_1)\) cắt \((O_2)\) tại \(A;\) \((O_1)\) cắt \((O_3)\) tại \(B.\)
\((O_2)\) cắt \((O_3)\) tại \(C.\) Suy ra \(D\) là điểm nằm trên đường tròn \((O_3).\)
\(BD\) cắt \((O_1)\) tại \(M,\) \(DC\) cắt \((O_2)\) tại \(N.\)
Nối \(PA, PB, PC,\) \(MA, NA.\)
Ta có tứ giác \(APBM\) nội tiếp trong đường tròn \((O_1).\)
Nên \(\widehat {MAP} + \widehat {MBP} = 180^\circ \) (tính chất tứ giác nội tiếp)
Mà \(\widehat {MBP} + \widehat {PBD} = 180^\circ \) (hai góc kề bù)
Suy ra: \(\widehat {MAP} = \widehat {PBD}\) \( (1)\)
Ta có: Tứ giác \(APCN\) nội tiếp trong đường tròn \((O_2)\)
Nên \(\widehat {NAP} + \widehat {NCP} = 180^\circ \) (tính chất tứ giác nội tiếp)
Mà \(\widehat {NCP} + \widehat {PCD} = 180^\circ \) (hai góc kề bù)
Suy ra: \(\widehat {NAP} = \widehat {PCD}\) \( (2)\)
Tứ giác \(BPCD\) nội tiếp trong đường tròn \((O_3)\)
\( \Rightarrow \widehat {PBD} + \widehat {PCD} = 180^\circ \) (tính chất tứ giác nội tiếp) \((3)\)
Từ \((1),\) \((2)\) và \((3)\) suy ra: \(\widehat {MAP} + \widehat {NAP} = 180^\circ \)
Vậy ba điểm \(M, A, N\) thẳng hàng.
-- Mod Toán 9 HỌC247
-


Chứng minh rằng AMBN nội tiếp đường tròn
bởi thủy tiên
 28/01/2019
28/01/2019
cho đường tròn(O;R) đường kính AB.Vẽ đường kính MN của đường tròn (M≠A,M≠B). Tiếp tuyến của đường tròn tại B cắt các đường thẳng AM, AN Lần lượt tại Q,P.
a, CM: AMBN nội tiếp đường tròn
b, CM: M,N,P,Q cùng thuộc 1 đường tròn
c, Gọi E là trung điểm của BQ. Đường thẳng vuông góc với OE tại O cắt PQ tại F.CM F là trung điểm của BP và ME song song NF
Theo dõi (0) 1 Trả lời -


Chứng minh tứ giác AHDI, HDIE nội tiếp
bởi minh vương
 28/01/2019
28/01/2019
Cho \(\Delta\) ABC vuông tại A. Từ một điểm D trên cạnh BC, vẽ DH \(\perp\) AC, DK \(\perp\) HI. Trên tia DK lấy điểm E sao cho K là trung điểm của DE. Chứng minh:
a) Tứ giác AHDI, HDIE nội tiếp
b) Năm điểm A,H,D,I và E cùng nằm trên 1 đường tròn
Mình đang cần gấp. HELP !!! T_T T_T T_T
Theo dõi (0) 1 Trả lời -


Chứng minh tam giác DEF có 3 góc nhọn
bởi Vũ Hải Yến
 28/01/2019
28/01/2019
Cho tam giác ABC cân tại A, đường tròn tâm O tiếp xúc (trong) với các cạnh AB, BC, CA lần lượt tại các điểm D, E, F. BF cắt đường tròn tâm O tại I, DI cắt BC tại M.
a) Chứng minh tam giác DEF có 3 góc nhọn.
b) DF//BC.
c) Tứ giác BDFC nội tiếp.
d) BD/CB = BM/CF.Theo dõi (0) 1 Trả lời -


Chứng minh tứ giác CGHF nội tiếp
bởi Nguyễn Trà Long
 28/01/2019
28/01/2019
Cho đường tròn (O) đường kính AB.Từ một điểm M thuộc tia đối của tia AB,vẽ tiếp tuyến MC,MD (C,D \(\in\)(O)).Vẽ \(CE\perp DB\) tại E.Gọi F là trung điểm của CE,BF cắt (O) tại điểm thứ hai G.Gọi H là giao điểm của AB và CD.Chứng minh:
a)Tứ giác CGHF nội tiếp.
b) Tứ giác MGHD nội tiếp.
c) BM tiếp xúc với đường tròn ngoại tiếp \(\Delta MGC\).
d) Cho CG cắt MH tại S.Chứng minh S là trung điểm của MH.
Theo dõi (0) 1 Trả lời -


Chứng minh ABOC là tứ giác nội tiếp
bởi Phan Thiện Hải
 28/01/2019
28/01/2019
Cho điểm A nằm bên ngoài đường tròn (O). Từ A kẻ hai tiếp tuyến AB, AC với đường tròn đó. (B, C là các tiếp điểm). Gọi M là trung điểm của AB. Đường thẳng MC cắt đường tròn (O) tại N (N khác C).
a, Chứng minh ABOC là tứ giác nội tiếp.
b, chứng minh MB2 = MN.MC
c, Tia AN cắt đường tròn (O) tại D (D khác N). Chứng minh góc MAN = góc ADCTheo dõi (0) 1 Trả lời -


Chứng minh tam giác ABE vuông biết E là giao điểm của đường thẳng BI với AJ
bởi Lê Tường Vy
 04/04/2019
04/04/2019
Cho tam giác ABC vuông tại a kẻ đường cao AH đường phân giác AD . Gọi I, J lần lượt là giao điểm các phân giác của các tam giác ABH và ACH . Gọi E là giao điểm của đường thẳng BI với AJ.
Cm : a/. ABE là tam giác vuông
b/. Cm : IJ và AD vuông góc với nhau
Theo dõi (0) 1 Trả lời -


Chứng minh rằng các tứ giác AECD, BFCD nội tiếp
bởi thu hằng
 28/01/2019
28/01/2019
Bài 2 Từ 1 điểm M ở bên ngoài đường tròn (O) ta vẽ hai tiếp tuyến MA, MB với đường tròn. Trên cung nhỏ AB lấy một điểm C. Vẽ CD, CE, CF lầm lượt vuông góc với AB, MA, MB . Gọi I là giao đieme của AC và DE , K là giao điểm của BC và DF. Chứng minh rằng:
a: các tứ giác AECD , BFCD nội tiếp
b: CD2 =CE× CF
c: tứ giác ICKD nội tiếp
Theo dõi (0) 1 Trả lời -


Chứng minh tứ giác AHIK nội tiếp
bởi Thanh Truc
 28/01/2019
28/01/2019
Cho tam giác ABC nội tiếp đường tròn tâm O, I là giao điêmcủa hai đường cao BH và CK. Chứng minh:
a) Tứ giác AHIK nội tiếp.b) góc CAI bằng góc BCH
Theo dõi (0) 1 Trả lời -


Chứng minh tứ giác BCDE nội tiếp được đường tròn, từ đó suy ra góc BCD = góc AED
bởi Hong Van
 29/01/2019
29/01/2019
giải dùm mk câu a) vs. Mk cảm ơn nhiều
Cho tam giác ABC có ba góc nhọn nội tiếp trong đường tròn tâm O. Các đường cao BD và CE của tam giác (D thuộc AC, E thuộc AB) cắt nhau tại H. Chứng minh:
a)Tứ giác BCDE nội tiếp được đường tròn, từ đó suy ra góc BCD = góc AED
Theo dõi (0) 1 Trả lời -


Chứng minh BEFI nội tiếp
bởi Nguyễn Phương Khanh
 29/01/2019
29/01/2019
Cho (O) đkính AB.Vẽ dây CD vuông với AB tại I (I nằm giữa A và O).Lấy E thuộc cung BC nhỏ (E khác B,C) AE cắt CD tại F
a)Chứng minh BEFI nội tiếp
b) AE×AF=AC^2
Theo dõi (0) 1 Trả lời -


Cho tam giác ABC, góc A bằng 90 độ, AH vuông BC, Biết \(\dfrac{AB}{AC}=\dfrac{1}{\sqrt{3}},HC-HB=8\)
a) tính các cạnh của tam giác ABC ?
b) Hình chữ nhật MNIQ nội tiếp tam giác ABC (I,Q thuộc BC ; M thuộc AB ; N thuộc AC). Tìm giá trị lớn nhất của \(S_{MINQ}?\)
Theo dõi (0) 1 Trả lời





