Phß║¦n hŲ░ß╗øng dß║½n giß║Żi b├Āi tß║Łp SGK H├¼nh hß╗Źc 9 B├Āi 7 Tß╗® gi├Īc nß╗Öi tiß║┐p sß║Į gi├║p c├Īc em nß║»m ─æŲ░ß╗Żc phŲ░ŲĪng ph├Īp v├Ā r├©n luyß╗ćn k─® n─āng c├Īc dß║Īng b├Āi tß║Łp tß╗½ SGK To├Īn 9.
-
B├Āi tß║Łp 53 trang 89 SGK To├Īn 9 Tß║Łp 2
Biß║┐t ABCD l├Ā tß╗® gi├Īc nß╗Öi tiß║┐p. H├Ży ─æiß╗ün v├Āo ├┤ trß╗æng trong bß║│ng sau (nß║┐u c├│ thß╗ā)
-
B├Āi tß║Łp 54 trang 89 SGK To├Īn 9 Tß║Łp 2
Tß╗® gi├Īc ABCD c├│ \(\small \widehat{ABC}+\widehat{ADC}=180^o\). Chß╗®ng minh rß║▒ng c├Īc ─æŲ░ß╗Øng trung trß╗▒c cß╗¦a AC, BD, AB c├╣ng ─æi qua mß╗Öt ─æiß╗ām.
-
B├Āi tß║Łp 55 trang 89 SGK To├Īn 9 Tß║Łp 2
Cho ABCD l├Ā mß╗Öt tß╗® gi├Īc nß╗Öi tiß║┐p ─æŲ░ß╗Øng tr├▓n t├óm M, biß║┐t:
\(\small \widehat{DAB}=80^o,\widehat{DAM}=30^o,\widehat{BMC}=70^o\)
H├Ży t├Łnh sß╗æ ─æo c├Īc g├│c:
\(\widehat{MAB},\widehat{BCM},\widehat{AMB},\widehat{DMC},\widehat{AMD},\widehat{MCD},\widehat{BCD}\)
-
B├Āi tß║Łp 56 trang 89 SGK To├Īn 9 Tß║Łp 2
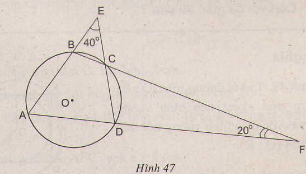
Xem h├¼nh 47. H├Ży t├¼m sß╗æ ─æo c├Īc g├│c cß╗¦a tß╗® gi├Īc ABCD
-
B├Āi tß║Łp 57 trang 89 SGK To├Īn 9 Tß║Łp 2
Trong c├Īc h├¼nh sau, h├¼nh n├Āo nß╗Öi tiß║┐p ─æŲ░ß╗Żc mß╗Öt ─æŲ░ß╗Øng tr├▓n: H├¼nh b├¼nh h├Ānh, h├¼nh chß╗» nhß║Łt, h├¼nh vu├┤ng, h├¼nh thang, h├¼nh thang vu├┤ng, h├¼nh thang c├ón ? V├¼ sao?
-
B├Āi tß║Łp 58 trang 90 SGK To├Īn 9 Tß║Łp 2
Cho tam gi├Īc ─æß╗üu ABC. Tr├¬n nß╗Ła mß║Ęt phß║│ng bß╗Ø BC kh├┤ng chß╗®a ─æß╗ēnh A, lß║źy ─æiß╗ām D sao cho DB = DC v├Ā
\(\small \widehat{DCB}=\frac{1}{2}\widehat{ACB}\)
a) Chß╗®ng minh ABDC l├Ā tß╗® gi├Īc nß╗Öi tiß║┐p
b) X├Īc ─æß╗ŗnh t├óm cß╗¦a ─æŲ░ß╗Øng tr├▓n ─æi qua bß╗æn ─æiß╗ām A, B, D, C.
-
B├Āi tß║Łp 59 trang 90 SGK To├Īn 9 Tß║Łp 2
Cho h├¼nh b├¼nh h├Ānh ABCD. ─ÉŲ░ß╗Øng tr├▓n ─æi qua ba ─æß╗ēnh A, B, C cß║»t ─æŲ░ß╗Øng thß║│ng CD tß║Īi P kh├Īc C. Chß╗®ng minh AP = AD
-
B├Āi tß║Łp 60 trang 90 SGK To├Īn 9 Tß║Łp 2
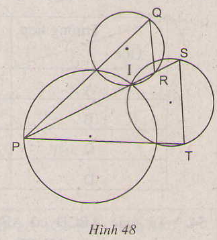
Xem h├¼nh 48. Chß╗®ng minh QR // ST.
-
B├Āi tß║Łp 39 trang 106 SBT To├Īn 9 Tß║Łp 2
Tr├¬n ─æŲ░ß╗Øng tr├▓n t├óm \(O\) c├│ mß╗Öt cung \(AB\) v├Ā \(S\) l├Ā ─æiß╗ām ch├Łnh giß╗»a cß╗¦a cung ─æ├│. Tr├¬n d├óy \(AB\) lß║źy hai ─æiß╗ām \(E\) v├Ā \(H.\) C├Īc ─æŲ░ß╗Øng thß║│ng \(SH\) v├Ā \(SE\) cß║»t ─æŲ░ß╗Øng tr├▓n theo thß╗® tß╗▒ tß║Īi \(C\) v├Ā \(D.\) Chß╗®ng minh \(EHCD\) l├Ā mß╗Öt tß╗® gi├Īc nß╗Öi tiß║┐p.
-
B├Āi tß║Łp 40 trang 106 SBT To├Īn 9 Tß║Łp 2
Cho tam gi├Īc \(ABC.\) C├Īc ─æŲ░ß╗Øng ph├ón gi├Īc trong cß╗¦a \(\widehat B\) v├Ā \(\widehat C\) cß║»t nhau tß║Īi \(S,\) c├Īc ─æŲ░ß╗Øng ph├ón gi├Īc ngo├Āi cß╗¦a \(\widehat B\) v├Ā \(\widehat C\) cß║»t nhau tß║Īi \(E.\) Chß╗®ng minh \(BSCE\) l├Ā mß╗Öt tß╗® gi├Īc nß╗Öi tiß║┐p.
-
B├Āi tß║Łp 41 trang 106 SBT To├Īn 9 Tß║Łp 2
Cho tam gi├Īc c├ón \(ABC\) c├│ ─æ├Īy \(BC\) v├Ā \(\widehat A = {20^0}\). Tr├¬n nß╗Ła mß║Ęt phß║│ng bß╗Ø \(AB\) kh├┤ng chß╗®a ─æiß╗ām \(C\) lß║źy ─æiß╗ām \(D\) sao cho \(DA = DB\) v├Ā \(\widehat {DAB} = {40^0}\). Gß╗Źi \(E\) l├Ā giao ─æiß╗ām cß╗¦a \(AB\) v├Ā \(CD.\)
\(a)\) Chß╗®ng minh \(ACBD\) l├Ā tß╗® gi├Īc nß╗Öi tiß║┐p
\(b)\) T├Łnh \(\widehat {AED}\)
-
B├Āi tß║Łp 42 trang 107 SBT To├Īn 9 Tß║Łp 2
Cho ba ─æŲ░ß╗Øng tr├▓n c├╣ng ─æi qua mß╗Öt ─æiß╗ām \(P.\) Gß╗Źi c├Īc giao ─æiß╗ām kh├Īc \(P\) cß╗¦a hai trong ba ─æŲ░ß╗Øng tr├▓n ─æ├│ l├Ā \(A, B, C.\) Tß╗½ mß╗Öt ─æiß╗ām \(D\) (kh├Īc ─æiß╗ām \(P\)) tr├¬n ─æŲ░ß╗Øng tr├▓n \((PBC)\) kß║╗ c├Īc tia \(DB, DC\) cß║»t c├Īc ─æŲ░ß╗Øng tr├▓n \((PAB)\) v├Ā \((PAC)\) lß║¦n lŲ░ß╗Żt tß║Īi \(M, N.\) Chß╗®ng minh ba ─æiß╗ām \(M, A, N\) thß║│ng h├Āng.
-
B├Āi tß║Łp 43 trang 107 SBT To├Īn 9 Tß║Łp 2
Cho hai ─æoß║Īn thß║│ng \(AC\) v├Ā \(BD\) cß║»t nhau tß║Īi \(E.\) Biß║┐t \(AE.EC = BE.ED\). Chß╗®ng minh bß╗æn ─æiß╗ām \(A, B, C, D \)c├╣ng nß║▒m tr├¬n mß╗Öt ─æŲ░ß╗Øng tr├▓n.
-
B├Āi tß║Łp 7.1 trang 107 SBT To├Īn 9 Tß║Łp 2
Cho tam gi├Īc \(ABC\) c├│ ba g├│c nhß╗Źn. Vß║Į c├Īc ─æŲ░ß╗Øng cao \(AI, BK, CL\) cß╗¦a tam gi├Īc ß║źy.Gß╗Źi \(H\) l├Ā giao ─æiß╗ām cß╗¦a c├Īc ─æŲ░ß╗Øng cao vß╗½a vß║Į.
\(a)\) Chß╗ē ra c├Īc tß╗® gi├Īc nß╗Öi tiß║┐p c├│ ─æß╗ēnh lß║źy trong sß╗æ c├Īc ─æiß╗ām \(A, B, C, H, I, K, L\)
\(b)\) Chß╗®ng minh \(\widehat {LBH},\widehat {LIH},\widehat {KIH}\) v├Ā \(\widehat {KCH}\) l├Ā \(4\) g├│c bß║▒ng nhau.
\(c)\) Chß╗®ng minh \(KB\) l├Ā tia ph├ón gi├Īc cß╗¦a \(\widehat {LKI}.\)
-
B├Āi tß║Łp 7.2 trang 107 SBT To├Īn 9 Tß║Łp 2
Cho ─æŲ░ß╗Øng tr├▓n t├óm \(O\) b├Īn k├Łnh \(R\) v├Ā hai d├óy \(AB,\) \(CD\) bß║źt k├¼. Gß╗Źi \(M\) l├Ā ─æiß╗ām ch├Łnh giß╗»a cß╗¦a cung nhß╗Å \(AB.\) Gß╗Źi \(E\) v├Ā \(F\) tŲ░ŲĪng ß╗®ng l├Ā giao ─æiß╗ām cß╗¦a \(MC,\) \(MD\) vß╗øi d├óy \(AB.\) Gß╗Źi \(I\) v├Ā \(J\) tŲ░ŲĪng ß╗®ng l├Ā giao ─æiß╗ām cß╗¦a \(DE,\) \(CF\) vß╗øi ─æŲ░ß╗Øng tr├▓n \((O).\) Chß╗®ng minh \(IJ\) song song vß╗øi \(AB.\)






