Bài tập 1 trang 156 SBT Toán 9 Tập 1
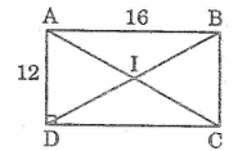
Cho hình chữ nhật ABCD có AD = 12cm, CD = 16cm. Chứng minh rằng bốn điểm ABCD cùng thuộc một đường tròn.Tính bán kính của đường tròn đó.
Hướng dẫn giải chi tiết
Gọi I là giao điểm của hai đường chéo AC và BD. Ta có:
IA = IB = IC = ID (tính chất hình chữ nhật)
Vậy bốn điểm A, B, C, D cùng nằm trên một đường tròn bán kính AC/2
Áp dụng định lí Pitago vào tam giác vuông ABC ta có:
AC2 = AB2 + BC2 = 162 + 122 = 256 + 144 = 400
Suy ra: AC = √400 = 20 (cm)
Vậy bán kính đường tròn là: IA = AC/2 = 20/2 = 10 (cm)
-- Mod Toán 9 HỌC247
-


Chứng minh rằng CD⊥AB, BE⊥ AC
bởi Ban Mai
 22/01/2019
22/01/2019
cho △ABC nhọn vẽ (O) đường kính BC cắt các cạnh AB,AC thao thứ tự D,E.
a, C/m CD⊥AB, BE⊥ AC.
b, gọi K là giao điểm của CD và BE . C/ m AK⊥ BC.
c, C/m góc BAK = góc BED
d, C/m BK.DE + CK.CD= BC2
Theo dõi (0) 2 Trả lời -


Cho tam giác ABC cân tại A, các đường cao AD và BE cắt nhau tại H.
a, Chứng minh 4 điểm A,E, D, B cùng nằm trên một đường tròn.
b, Chứng minh tam giác BDE là tam giác cân.
c, Gọi O là tâm của đường tròn ngoại tiếp tam giác AHE . Chứng minh DE là tiếp tuyến của đường tròn O.
Theo dõi (0) 1 Trả lời -


Chứng minh AC là tiếp điểm của đường tròn
bởi Trần Hoàng Mai
 22/01/2019
22/01/2019
1: Cho tam giác ABC có AB = 6m , AC = 8cm , BC = 10cm . Vẽ đương tròn ( B;BA ) . Chứng minh AC là tiếp điểm của đường tròn
2: Cho tam giác ABC cân tại A đường cao AH và BK cắt nhau tại I . Chứng minh
a, đường tròn đường kính AI đi qua K
b, HK là tiếp tuyến của đường tròn AI
@tran trong bac help me ná
@phynit , @Nguyễn Huy Tú , ....
Các bạn trên hoc24 nữa ạ !
Theo dõi (0) 1 Trả lời
Bài tập SGK khác
Bài tập 8 trang 101 SGK Toán 9 Tập 1
Bài tập 9 trang 101 SGK Toán 9 Tập 1
Bài tập 2 trang 156 SBT Toán 9 Tập 1
Bài tập 3 trang 156 SBT Toán 9 Tập 1
Bài tập 4 trang 156 SBT Toán 9 Tập 1
Bài tập 5 trang 156 SBT Toán 9 Tập 1
Bài tập 6 trang 157 SBT Toán 9 Tập 1
Bài tập 7 trang 157 SBT Toán 9 Tập 1
Bài tập 8 trang 157 SBT Toán 9 Tập 1
Bài tập 9 trang 157 SBT Toán 9 Tập 1
Bài tập 10 trang 157 SBT Toán 9 Tập 1
Bài tập 11 trang 157 SBT Toán 9 Tập 1
Bài tập 12 trang 158 SBT Toán 9 Tập 1
Bài tập 13 trang 158 SBT Toán 9 Tập 1
Bài tập 14 trang 158 SBT Toán 9 Tập 1
Bài tập 1.1 trang 158 SBT Toán 9 Tập 1