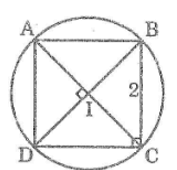
Bài tập 11 trang 157 SBT Toán 9 Tập 1
Cho hình vuông ABCD.
a. Chứng minh rằng bốn đỉnh của hình vuông cùng nằm trên một đường tròn. Hãy chỉ ra vị trí của tâm đường tròn đó
b. Tính bán kính của đường tròn đó, biết cạnh của hình vuông bằng 2cm.
Hướng dẫn giải chi tiết
a. Gọi I là giao điểm của hai đường chéo AC và BD.
Ta có: IA = IB = IC = ID (tính chất của hình vuông)
Vậy bốn điểm A, B, C, D cùng nằm trên một đường tròn. Tâm của đường tròn là I.
b. Áp dụng định lí Pitago vào tam giác vuông ABC ta có:
AC2 = AB2 + BC2 = 22 + 22 = 8
Suy ra: AC = 2√2 (cm)
-- Mod Toán 9 HỌC247
-
Bài 2 trang 156 sách bài tập toán 9 tập 1
bởi thu phương
10/10/2018
Bài 2 (Sách bài tập trang 156)
Trên mặt phẳng tọa độ Oxy, hãy xác định vị trí tương đối của mỗi điển \(A\left(1;-1\right),B\left(-\sqrt{2};\sqrt{2}\right)\) và \(C\left(1;1\right)\) đối với đường tròn (O; 2) ?
Theo dõi (0) 1 Trả lời -
Bài 1 trang 156 sách bài tập toán 9 tập 1
bởi minh dương
10/10/2018
Bài 1 (Sách bài tập trang 156)
Cho hình chữ nhật ABCD có AD = 12 cn, CD = 16cm. Chứng minh rằng bốn điểm ABCD thuộc cùng một đường tròn. Tính bán kính của đường tròn đó ?
Theo dõi (0) 1 Trả lời -
Chứng minh tâm của đường tròn ngoại tiếp tam giác vuông là trung điểm cạnh huyền
bởi Phạm Khánh Ngọc
24/07/2018
Bạn nào làm giúp mình với:Chứng minh tâm của đường tròn ngoại tiếp tam giác vuông là trung điểm cạnh huyền
Theo dõi (0) 2 Trả lời
