Bài học trước là các tính chất xoay quanh góc có đỉnh nằm trên đường tròn, hay còn gọi là góc nội tiếp. Còn ở bài này, ta sẽ đi tìm hiểu về Góc có đỉnh ở bên trong đường tròn. Góc có đỉnh ở bên ngoài đường tròn
Tóm tắt lý thuyết
1.1. Góc có đỉnh bên trong đường tròn
ĐỊNH LÍ: Số đo của góc có đỉnh bên trong đường tròn bẳng nửa tổng số đo hai cung bị chắn.
.png)
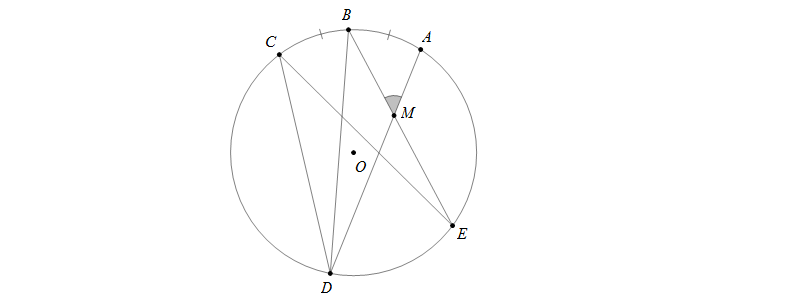
Góc \(\widehat{BEC}\) là góc có đỉnh \(E\) nằm bên trong đường tròn nên \(\widehat{BEC}=\frac{1}{2}\)(sđ\(\stackrel\frown{BnC}\)+sđ\(\stackrel\frown{AmD}\))
1.2. Góc có đỉnh bên ngoài đường tròn
ĐỊNH LÍ: Số đo của góc có đỉnh bên ngoài đường tròn bằng nửa hiệu số đo hai cung bị chắn.
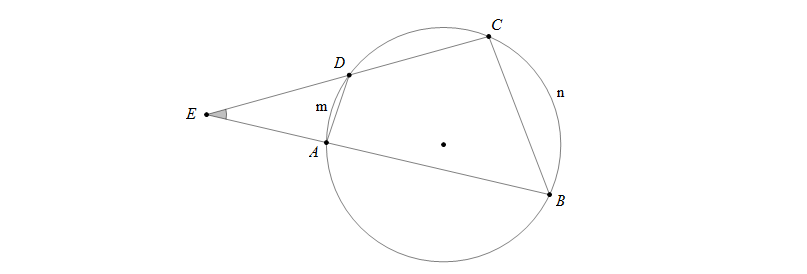
Góc \(\widehat{AED}\) có đỉnh \(E\) bên ngoài đường tròn nên \(\widehat{AED}=\frac{1}{2}\)(sđ\(\stackrel\frown{BnC}-\)sđ\(\stackrel\frown{AmD}\))
Bài tập minh họa
2.1. Bài tập cơ bản
Bài 1: Cho tam giác ABC cân tại A nội tiếp đường tròn tâm O. Điểm D di chuyển trên cung AC. E là diao điểm của AC và BD, F là giao điểm của AD và BC. Chứng minh \(\widehat{AFB}=\widehat{ABD}\)
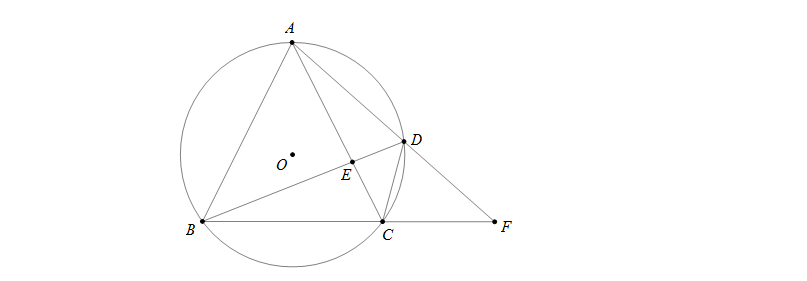
Hướng dẫn:
Do \(\bigtriangleup ABC\) cân tại A nên AB=AC suy ra sđ\(\stackrel\frown{AB}=\)sđ\(\stackrel\frown{AC}\)
Ta có \(\widehat{AFB}=\frac{1}{2}\)(sđ\(\stackrel\frown{AB}-\) sđ\(\stackrel\frown{CD}\))\(=\frac{1}{2}\)(sđ\(\stackrel\frown{AC}-\) sđ\(\stackrel\frown{CD}\))\(=\frac{1}{2}\)sđ\(\stackrel\frown{AD}\)
Mặt khác \(\widehat{ABD}=\frac{1}{2}\)sđ\(\stackrel\frown{AD}\), do đó \(\widehat{AFB}=\widehat{ABD}\)
Bài 2: Cho tam giác ABC nội tiếp đường tròn tâm O. Gọi P,Q,R lần lượt là giao điểm của các tia phân giác trong góc A,B,C với đường tròn. Chứng minh \(AP\perp QR\)
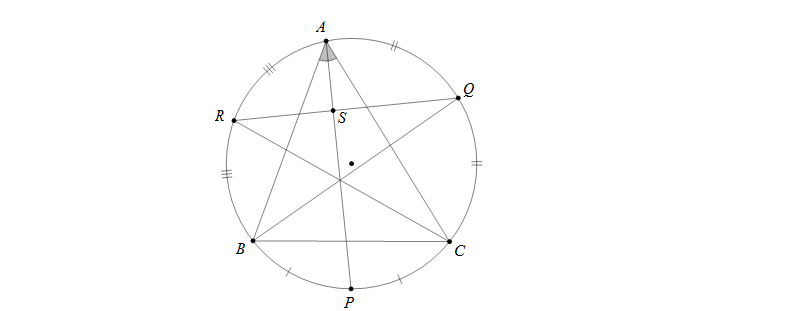
Hướng dẫn:
Ta có tia phân giác AP chia đôi cung \(\stackrel\frown{BC}\) thành hai cung bằng nhau, tức là \(\stackrel\frown{BP}=\stackrel\frown{CP}\)
Tương tự \(\stackrel\frown{AQ}=\stackrel\frown{CQ},\stackrel\frown{AR}=\stackrel\frown{BR}\)
Gọi S là giao điểm của AP và QR. Lúc đó \(\widehat{ASQ}=\frac{1}{2}\)(sđ\(\stackrel\frown{AQ}+\)sđ\(\stackrel\frown{PR}\))\(=\frac{1}{2}(\frac{1}{2}\)sđ\(\stackrel\frown{AC}\)+\(\frac{1}{2}\)sđ\(\stackrel\frown{AB}\)+\(\frac{1}{2}\)sđ\(\stackrel\frown{BC})\)=\(\frac{1}{2}.(\frac{1}{2}.360^0)=90^0\)
Và do đó \(AP\perp QR\)
Bài 3: Cho tam giác nhọn ABC (AB>BC) nội tiếp đường tròn (O). D là điểm chính giữa cung AC. Gọi E,F lần lượt là giao điểm của AB và CD; AD và BC. Chứng minh rằng \(\widehat{AED}<\widehat{CFD}\)
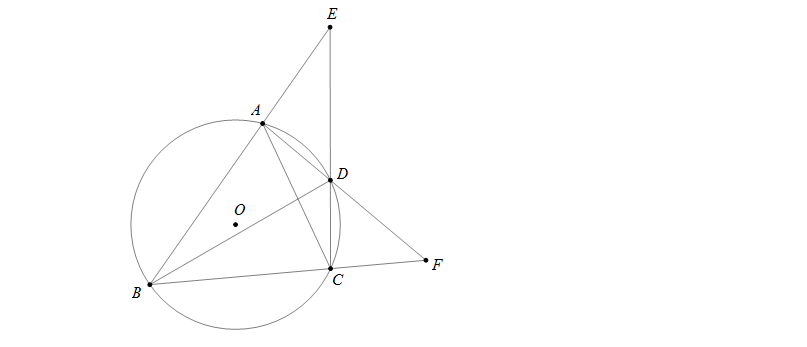
Hướng dẫn:
Ta có: \(\widehat{AED}=\frac{1}{2}\)(sđ\(\stackrel\frown{BC}-\)sđ\(\stackrel\frown{AD}\)) và \(\widehat{CFD}=\frac{1}{2}\)(sđ\(\stackrel\frown{AB}-\)sđ\(\stackrel\frown{CD}\))
Theo đề bài ta có sđ\(\stackrel\frown{BC}<\)sđ\(\stackrel\frown{AB}\) (do AB>BC) và sđ\(\stackrel\frown{AD}\)=sđ\(\stackrel\frown{CD}\) (do D là điểm chính giữa cung AC)
Suy ra\(\widehat{AED}<\widehat{CFD}\)
2.2. Bài tập nâng cao
Bài 1: Cho tam giác đều ABC nội tiếp đường tròn tâm O. D là một điểm di dộng trên cung nhỏ AC. Gọi E là giao điểm của AC và BD, gọi F là giao điểm của AD và BC. Chứng minh tích AE.BF không phụ thuộc vào vị trí của D

Hướng dẫn:
Vì AB=AC nên sđ\(\stackrel\frown{AB}=\)sđ\(\stackrel\frown{AC}\)
Ta có \(\widehat{AFB}=\frac{1}{2}\)(sđ\(\stackrel\frown{AB}-\) sđ\(\stackrel\frown{CD}\))\(=\frac{1}{2}\)(sđ\(\stackrel\frown{AC}-\) sđ\(\stackrel\frown{CD}\))\(=\frac{1}{2}\)sđ\(\stackrel\frown{AD}\)
Mặt khác \(\widehat{ABD}=\frac{1}{2}\)sđ\(\stackrel\frown{AD}\), do đó \(\widehat{AFB}=\widehat{ABD}\)
Xét \(\bigtriangleup AFB\) và \(\bigtriangleup EBA\) có \(\widehat{AFB}=\widehat{ABD}\) (chứng minh trên) và \(\widehat{FBA}=\widehat{BAE}=60^0\) (\(\bigtriangleup ABC\) đều)
nên \(\bigtriangleup AFB \sim\bigtriangleup EBA\) (g.g) suy ra \(\frac{AB}{AE}=\frac{BF}{AB} \Rightarrow AE.BF=AB^2\) không đổi
Vậy tích AE.BF không phụ thuộc vào vị trí điểm D
Bài 2: Tứ giác ABCD có các góc B và D tù. Chứng minh AC>BD

Hướng dẫn:
Vẽ đường tròn tâm O đường kính AC.
Ta có \(\widehat{ABC}>90^0, \widehat{ADC}>90^0\) nên B và D là hai điểm ở bên trong đường tròn (O)
suy ra BD nhỏ hơn dây cung chứa nó
Mặt khác đường kính AC là dây cung lớn nhất và do đó AC>BD
3. Luyện tập Bài 5 Chương 3 Hình học 9
Qua bài giảng Góc có đỉnh ở bên trong đường tròn Góc có đỉnh ở bên ngoài đường tròn này, các em cần hoàn thành 1 số mục tiêu mà bài đưa ra như :
- Nắm vững lý thuyết về góc có đỉnh ở bên trong đường tròn, góc có đỉnh ở bên ngoài đường tròn
- Vận dụng lý thuyết làm được một số bài tập
3.1 Trắc nghiệm về Góc có đỉnh ở bên trong đường tròn Góc có đỉnh ở bên ngoài đường tròn
Để cũng cố bài học xin mời các em cũng làm Bài kiểm tra Trắc nghiệm Hình học 9 Bài 5 để kiểm tra xem mình đã nắm được nội dung bài học hay chưa.
-
- A. 900
- B. 600
- C. 450
- D. 500
-
Câu 2:
Khẳng nào sau đây là đúng:
- A. Số đo của góc có đỉnh bên trong đường tròn bằng nửa hiệu số đo hai cung bị chắn.
- B. Số đo của góc có đỉnh bên ngoài đường tròn bằng nửa tổng số đo hai cung bị chắn.
- C. Góc có đỉnh trên đường tròn được gọi là góc nội tiếp và bằng góc ở tâm cùng chắn cung đó.
- D. Góc nội tiếp chắn nửa đường tròn là góc vuông.
Câu 3-5: Mời các em đăng nhập xem tiếp nội dung và thi thử Online để củng cố kiến thức và nắm vững hơn về bài học này nhé!
3.2 Bài tập SGK về Góc có đỉnh ở bên trong đường tròn Góc có đỉnh ở bên ngoài đường tròn
Bên cạnh đó các em có thể xem phần hướng dẫn Giải bài tập Hình học 9 Bài 5 sẽ giúp các em nắm được các phương pháp giải bài tập từ SGK Toán 9 tập 1
Bài tập 36 trang 82 SGK Toán 9 Tập 2
Bài tập 37 trang 82 SGK Toán 9 Tập 2
Bài tập 38 trang 82 SGK Toán 9 Tập 2
Bài tập 39 trang 83 SGK Toán 9 Tập 2
Bài tập 40 trang 83 SGK Toán 9 Tập 2
Bài tập 41 trang 83 SGK Toán 9 Tập 2
Bài tập 42 trang 83 SGK Toán 9 Tập 2
Bài tập 43 trang 83 SGK Toán 9 Tập 2
Bài tập 28 trang 104 SBT Toán 9 Tập 2
Bài tập 29 trang 105 SBT Toán 9 Tập 2
Bài tập 30 trang 105 SBT Toán 9 Tập 2
Bài tập 31 trang 105 SBT Toán 9 Tập 2
Bài tập 32 trang 105 SBT Toán 9 Tập 2
Bài tập 5.1 trang 105 SBT Toán 9 Tập 2
Bài tập 5.2 trang 105 SBT Toán 9 Tập 2
4. Hỏi đáp Bài 5 Chương 3 Hình học 9
Nếu có thắc mắc cần giải đáp các em có thể để lại câu hỏi trong phần Hỏi đáp, cộng đồng Toán HỌC247 sẽ sớm trả lời cho các em.
-- Mod Toán Học 9 HỌC247