Bài tập 5.2 trang 105 SBT Toán 9 Tập 2

Hướng dẫn giải

Ta sử dụng kiến thức:

+) Với hai cung nhỏ trong một đường tròn, hai dây bằng nhau căng hai cung bằng nhau.

+) Trong một đường tròn, số đo góc nội tiếp bằng nửa số đo của cung bị chắn.

+) Nếu $C$ là một điểm trên cung $AB$ thì $sđ \overparen{AB}=sđ \overparen{AC}+sđ \overparen{CB}.$

+) Số đo của góc có đỉnh ở bên ngoài đường tròn bằng nửa hiệu số đo hai cung bị chắn.

Lời giải chi tiết

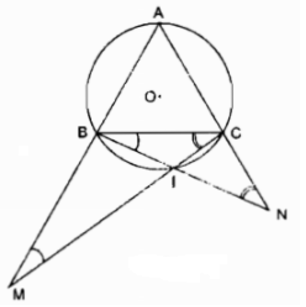
Vì $AB = AC = BC\;\; (gt)$

Suy ra các cung nhỏ $\overparen{AB} = \overparen{AC} = \overparen{BC}$   $(1)$

$a)$ Xét đường tròn $(O)$ có: $\widehat {BCI} = \displaystyle {1 \over 2} sđ \overparen{BI}$ (tính chất góc nội tiếp)

hay $\widehat {BCI} = \displaystyle{1 \over 2} (sđ \overparen{BC}- sđ \overparen{CI}$) $(2)$

Từ $(1)$ và $(2)$ suy ra: $\widehat {BCI} =\displaystyle {1 \over 2} (sđ \overparen{AB}- sđ \overparen{CI})$    $(3)$

Lại có: $\widehat {ANB} = \displaystyle {1 \over 2} (sđ \overparen{AB}- sđ \overparen{CI})$ (góc có ở đỉnh bên ngoài đường tròn) $(4)$

Từ $(3)$ và $(4)$ suy ra: $\widehat {ANB} = \widehat {BCI}$

$b)$ Xét đường tròn $(O)$ có:  $\widehat {CBI} =\displaystyle {1 \over 2} sđ \overparen{CI}$ (tính chất góc nội tiếp)

Hay $\widehat {CBI} = \displaystyle{1 \over 2} (sđ \overparen{BC}- sđ \overparen{BI}$) $(5)$

Từ $(1)$ và $(5)$ suy ra: $\widehat {CBI} = \displaystyle{1 \over 2} (sđ \overparen{AC}- sđ \overparen{BI}$) $(6)$

Lại có: $\widehat {AMC} = \displaystyle{1 \over 2} (sđ \overparen{AC}- sđ \overparen{BI}$) (góc có đỉnh bên ngoài đường tròn) $(7)$

Từ $(6)$ và $(7)$ suy ra: $\widehat {AMC} = \widehat {CBI}$.

-- Mod Toán 9 HỌC247