Bài tập 28 tr 104 sách BT Toán lớp 9 Tập 2
Các điểm \({A_1},{A_2},....,{A_{19}},{A_{20}}\) được sắp xếp theo thứ tự đó trên đường tròn \((O)\) và chia đường tròn thành \(20\) cung bằng nhau. Chứng minh rằng dây \({A_1}{A_8}\) vuông góc với dây \({A_3}{A_{16}}\).
Hướng dẫn giải chi tiết
Hướng dẫn giải
Ta sử dụng kiến thức:
+) Số đo của góc có đỉnh ở bên trong đường tròn bằng nửa tổng số đo hai cung bị chắn.
Lời giải chi tiết
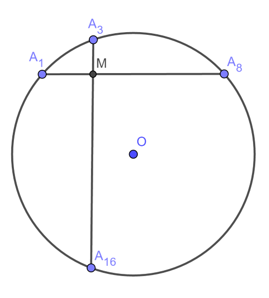
Đường tròn \((O)\) được chia thành \(20\) cung bằng nhau nên số đo mỗi cung bằng
\(360^o:20=18^o\)
Gọi giao điểm của \( A_1A_8\) và \( A_3A_{16}\) là \(I.\)
Ta có: \(sđ \overparen{{A_1}{A_3}}\) \( = {2.18^0} = {36^o}\)
\(sđ \overparen{{A_8}{A_{16}}}\) \( = {8.18^0} = {144^o}\)
Ta có: \(\widehat {{A_1}I{A_3}} = \displaystyle {1 \over 2} (sđ \overparen{{A_1}{A_3}} + sđ \overparen{{A_8}{A_{16}}})\) (góc có đỉnh ở trong đường tròn \((O)\))
\( \Rightarrow \) \(\widehat {{A_1}I{A_3}} = \displaystyle {{36^\circ + 144^\circ } \over 2} = 90^\circ \)
\( \Rightarrow A_1A_8 \bot A_3A_{16} \)
-- Mod Toán 9 HỌC247
-


Cho ∆ABM có góc AMB=60°,O là trung điểm AB.Tên cung chứa góc 60° dựng trên đoạn AB chứa M.lấy điểm N sao cho ON vuông góc AB. Chứng minh ∆ANB đều.
bởi Bảo Vânn
 20/03/2020
Giúp mk vs ạTheo dõi (0) 1 Trả lời
20/03/2020
Giúp mk vs ạTheo dõi (0) 1 Trả lời -


Từ 1 điểm M nằm bên ngoài (O) vẽ tiếp tuyến MA, cát tuyến MCB (C nằm giữa M và B ). Gọi N là điểm chính giữa của cung CB không chứa điểm A, AN cắt CB tại D. Chứng minh: a) MA=MD b) MA2 = MC.MBc, NB2= NA.ND
bởi Thu Tran
 13/03/2020
Từ 1 điểm M nằm bên ngoài (O) vẽ tiếp tuyến MA cát tuyến MCB (C nằm giữa M và B ) Gọi N là điểm chính giữa của cung CB không chứa điểm A, AN cắt CB tại D. CMinh:a, MA=MDb, MA2 = MC.MBc, NB2= NA.NDTheo dõi (0) 0 Trả lời
13/03/2020
Từ 1 điểm M nằm bên ngoài (O) vẽ tiếp tuyến MA cát tuyến MCB (C nằm giữa M và B ) Gọi N là điểm chính giữa của cung CB không chứa điểm A, AN cắt CB tại D. CMinh:a, MA=MDb, MA2 = MC.MBc, NB2= NA.NDTheo dõi (0) 0 Trả lời -


Tính góc A của tam giác ABC, có góc B=46 độ, góc C=72 độ
bởi Hoàng My
 22/01/2019
22/01/2019
Cho tam giác ABC nội tiếp đường tròn O có góc B=46 độ , góc C=72 độ
a) Tính góc A của tam giác ABC
b) Tia phâm giác góc A cắt đường tròn ở M. Tia phân giác góc B cắt đường tròn ở N. Gọi I là giao điểm của AM và BN. Tính các góc BIM, MBI
Theo dõi (0) 1 Trả lời





