Bài tập 5.1 tr 105 sách BT Toán lớp 9 Tập 2
Cho đường tròn tâm \(O \) bán kính \(R\) và dây \(AB\) bất kỳ. Gọi \(M\) là điểm chính giữa của cung nhỏ \(AB.\) \(E\) và \(F\) là hai điểm bất kỳ trên dây \(AB.\) Gọi \(C\) và \(D\) tương ứng là giao điểm của \(ME,\) \(MF\) của đường tròn \((O).\) Chứng minh \(\widehat {EFD} + \widehat {ECD} = {180^o}.\)
Hướng dẫn giải chi tiết
Hướng dẫn giải
Ta sử dụng kiến thức:
+) Trong một đường tròn, số đo góc nội tiếp bằng nửa số đo của cung bị chắn.
+) Nếu \(C\) là một điểm trên cung \(AB\) thì: \(sđ \overparen{AB}=sđ \overparen{AC}+sđ \overparen{CB}.\)
+) Số đo của góc có đỉnh ở bên ngoài đường tròn bằng nửa hiệu số đo hai cung bị chắn.
+) Tổng các góc trong một tứ giác bằng \(360^o.\)
Lời giải chi tiết
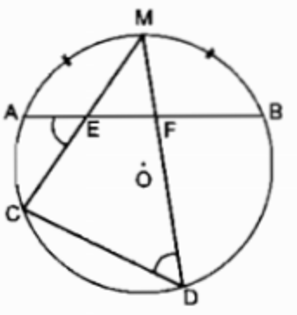
Ta có \(M\) là điểm chính giữa cung nhỏ \(\overparen{AB}\)
\( \Rightarrow sđ \overparen{MA} = sđ \overparen{MB}\) \((1)\)
Lại có: \(\widehat D = \displaystyle {1 \over 2} sđ \overparen{MAC}\) (tính chất góc nội tiếp)
\( \Rightarrow \) \(\widehat D = \displaystyle {1 \over 2} (sđ \overparen{MA} + sđ \overparen{AC}\)) \((2)\)
Và \(\widehat{AEC} =\displaystyle {1 \over 2}\) (sđ \(\overparen{MB}\) + sđ \(\overparen{AC}\)) (tính chất góc có đỉnh ở trong đường tròn) \( (3)\)
Từ \((1),\) \((2)\) và \((3)\) suy ra: \(\widehat D = \widehat {AEC}\)
\(\widehat {AEC} + \widehat {CEF} = 180^\circ \) (kề bù)
\( \Rightarrow \)\(\widehat D + \widehat {CEF} = 180^o \) \( (4)\)
Trong tứ giác \(CEFD\) ta có:
\(\widehat {CEF} + \widehat D + \widehat {ECD} + \widehat {EFD} = 360^o\) (tổng các góc trong tứ giác) \( (5)\)
Từ \((4)\) và \((5)\) suy ra: \(\widehat {ECD} + \widehat {EFD} = 180^o \)
-- Mod Toán 9 HỌC247
Chưa có câu hỏi nào. Em hãy trở thành người đầu tiên đặt câu hỏi.
