YOMEDIA
NONE
Trang chủ Toán 7

Bài tập 66 trang 146 SBT Toán 7 Tập 1

Lý thuyết10 Trắc nghiệm

23 BT SGK

328 FAQ

Giải bài 66 tr 146 sách BT Toán lớp 7 Tập 1

Cho tam giác \(ABC\) có \(\widehat A = 60^\circ \). Các tia phân giác của các góc \(B, C\) cắt nhau ở \(I\) và cắt \(AC, AB\) theo thứ tự ở \(D, E.\) Chứng minh rằng \(ID = IE.\)

Hướng dẫn: Kẻ tia phân giác của góc \(BIC\).

ATNETWORK

Hướng dẫn giải chi tiết

Hướng dẫn giải

- Nếu một cạnh và hai góc kề của tam giác này bằng một cạnh và hai góc kề của tam giác kia thì hai tam giác đó bằng nhau.

- Định lí tổng các góc của một tam giác bằng \(180^o\).

Lời giải chi tiết

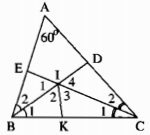
Trong ∆ABC, ta có:

\(\widehat A + \widehat B + \widehat C = 180^\circ \) (tổng 3 góc trong tam giác)

\( \Rightarrow \widehat B + \widehat C = 180^\circ  - \widehat A\)

                    \( = 180^\circ  - 60^\circ  = 120^\circ \)

\(\eqalign{
& \widehat {{B_1}} = \widehat {{B_2}} = {1 \over 2}\widehat B\left( {gt} \right) \cr
& \widehat {{C_1}} = \widehat {{C_2}} = {1 \over 2}\widehat C\left( {gt} \right) \cr} \)

Trong ∆BIC, ta có:

\(\widehat {BIC} = 180^\circ  - \left( {\widehat {{B_1}} + \widehat {{C_1}}} \right) = 180^\circ  - \left( {{{\widehat B} \over 2} + {{\widehat C} \over 2}} \right) = 180^\circ  - 60^\circ  = 120^\circ \)

Kẻ tia phân giác \(\widehat {BIC}\) cắt cạnh BC tại K

Suy ra: \(\widehat {{I_2}} = \widehat {{I_3}} = {1 \over 2}\widehat {BIC} = 60^\circ \)

Ta có: \(\widehat {{I_1}} + \widehat {BIC} = 180^\circ \) (hai góc kề bù)

\( \Rightarrow \widehat {{I_1}} = 180^\circ  - \widehat {BIC} = 180^\circ  - 120^\circ  = 60^\circ \)

\(\widehat {{I_4}} = \widehat {{I_1}} = 60^\circ \) (vì hai góc đối  đỉnh)

Xét ∆BIE và ∆BIK, ta có:  

\(\widehat {{B_1}} = \widehat {{B_2}}\left( {gt} \right)\)

BI cạnh chung  

\(\widehat {{I_1}} = \widehat {{I_2}} = 60^\circ \)

Suy ra: ∆BIE =  ∆BIK (g.c.g) => IE = IK (hai cạnh tương ứng)         (1)

Xét ∆CIK và ∆CID, ta có:

\(\widehat {{C_1}} = \widehat {{C_2}}\) (gt)

CI cạnh chung

\(\widehat {{I_3}} = \widehat {{I_4}} = 60^\circ \)

Suy ra: ∆CIK = ∆CID(g.c.g) => IK = ID (hai cạnh tương ứng)             (2)

Từ (1) và (2) suy ra: IE = ID.

-- Mod Toán 7 HỌC247

Nếu bạn thấy hướng dẫn giải Bài tập 66 trang 146 SBT Toán 7 Tập 1 HAY thì click chia sẻ 
YOMEDIA

Bài tập SGK khác

Bài tập 64 trang 146 SBT Toán 7 Tập 1

Bài tập 65 trang 146 SBT Toán 7 Tập 1

AANETWORK
 

XEM NHANH CHƯƠNG TRÌNH LỚP 7

 

YOMEDIA
ATNETWORK
ON