Phần hướng dẫn giải bài tập SGK Hình học 7 Chương 2 Bài 5 Trường hợp bằng nhau thứ ba của tam giác: góc - cạnh - góc (gcg) sẽ giúp các em nắm được phương pháp và rèn luyện kĩ năng các dạng bài tập từ SGK Toán 7 Tập một.
-
Bài tập 33 trang 123 SGK Toán 7 Tập 1
Vẽ tam giác ABC biết AC=2cm,
= 900
= 600
-
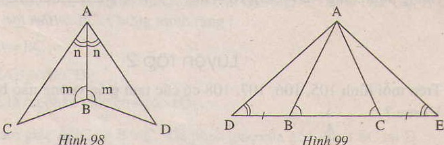
Bài tập 34 trang 123 SGK Toán 7 Tập 1
Trên mỗi hình 98,99 có tam giác nào bằng nhau? Vì sao?
-
Bài tập 35 trang 123 SGK Toán 7 Tập 1
Cho góc xOy khác góc bẹt, Ot là tia phân giác của góc đó. Qua H thuộc tia Ot , kẻ đường vuông góc với Ot, nó cắt Ox và Oy theo thứ tự A và B.
a) Chứng minh rằng OA=OB.
b ) Lấy điểm C thuộc tia Ot, chứng minh rằng CA=CB và
=
.
-
Bài tập 36 trang 123 SGK Toán 7 Tập 1
Trên hình 100 ta có OA=OB, OAC=OBD. Chứng minh rằng AC=BD.

-
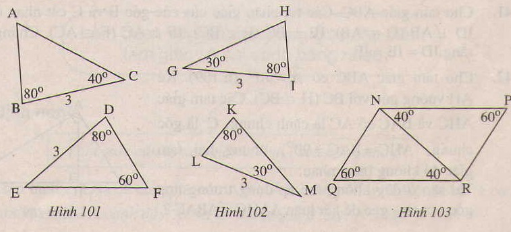
Bài tập 37 trang 123 SGK Toán 7 Tập 1
Trên mỗi hình 101,102,103 có tam giác nào bằng nhau? Vì sao?
-
Bài tập 49 trang 144 SBT Toán 7 Tập 1
Vẽ tam giác \(ABC\) biết \(\widehat B = 90^\circ ,BC = 2cm,\widehat C = 60^\circ \). Sau đó đo \(AC\) để kiểm tra rằng \(AC = 4cm.\)
-
Bài tập 50 trang 144 SBT Toán 7 Tập 1
Tìm các tam giác bằng nhau ở hình 55 (không xét tam giác mà các cạnh chưa được kẻ)
-
Bài tập 51 trang 144 SBT Toán 7 Tập 1
Cho tam giác \(ADE\) có \(\widehat D = \widehat E\). Tia phân giác của góc \(D\) cắt \(AE\) ở điểm \(M.\) Tia phân giác của góc \(E\) cắt \(AD\) ở điểm \(N\). So sánh các độ dài \(DN\) và \(EM.\)
-
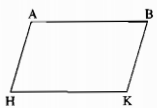
Bài tập 52 trang 144 SBT Toán 7 Tập 1
Cho hình 56, trong đó \(AB // HK, AH // BK.\) Chứng minh rằng \(AB = HK, AH = BK.\)
-
Bài tập 53 trang 144 SBT Toán 7 Tập 1
Cho tam giác \(ABC.\) Các tia phân giác của các góc \(B\) và \( C\) cắt nhau ở \(O.\) Kẻ \({\rm{OD}} \bot\, AC\), kẻ \({\rm{O}}E \bot \,AB\). Chứng minh rằng \(OD = OE.\)
-
Bài tập 54 trang 144 SBT Toán 7 Tập 1
Cho tam giác \(ABC\) có \(AB = AC.\) Lấy điểm \(D\) trên cạnh \(AB\), điểm \(E\) trên cạnh \(AC\) sao cho \(AD = AE.\)
a) Chứng minh rằng \( BE = CD.\)
b) Gọi \(O\) là giao điểm của \(BE\) và \(CD.\) Chứng minh rằng \(∆BOD = ∆COE\).
-
Bài tập 55 trang 145 SBT Toán 7 Tập 1
Cho tam giác \(ABC\) có \(\widehat B = \widehat C\). Tia phân giác góc \(A\) cắt \(BC\) tại \(D.\) Chứng minh rằng \(DB = DC, AB = AC.\)
-
Bài tập 56 trang 145 SBT Toán 7 Tập 1
Cho hình dưới, chứng minh rằng O là trung điểm của mỗi đoạn thẳng AD, BC
-
Bài tập 57 trang 145 SBT Toán 7 Tập 1
Cho hình 58 trong đó \(DE // AB, DF // AC, EF // BC.\) Tính chu vi tam giác \(DEF.\)
-
Bài tập 57 trang 145 SBT Toán 7 Tập 1
Cho đoạn thẳng \(AB.\) Qua \(A\) vẽ đường thẳng \(m\) vuông góc với \(AB.\) Qua \(B\) vẽ đường thẳng \(n\) vuông góc với \(AB.\) Qua trung điểm \(O\) của \(AB\) vẽ một đường thẳng cắt \(m\) ở \(C\) và cắt \(n\) ở \(D.\) So sánh các độ dài \(OC\) và \(OD.\)
-
Bài tập 59 trang 145 SBT Toán 7 Tập 1
Cho tam giác \(ABC\) có \(AB = 2,5cm, AC = 3cm, \) \(BC = 3,5cm.\) Qua \(A\) vẽ đường thẳng song song với \(BC\), qua \(C\) vẽ đường thẳng song song với \( AB\), chúng cắt nhau ở \(D.\) Tính chu vi tam giác \(ACD.\)
-
Bài tập 60 trang 145 SBT Toán 7 Tập 1
Cho tam giác \(ABC\) vuông tại \(A.\) Tia phân giác của góc \(B\) cắt \(AC\) ở \(D.\) Kẻ \(DE\) vuông góc với \(BC.\) Chứng minh rằng \(AB = BE.\)
-
Bài tập 61 trang 145 SBT Toán 7 Tập 1
Cho tam giác \(ABC\) vuông tại \(A\) có \(AB = AC.\) Qua \(A\) kẻ đường thẳng \(xy\) (\(B, C\) nằm cùng phía đối với \(xy\)). Kẻ \(BD\) và \(CE\) vuông góc với \(xy\). Chứng minh rằng:
a) \(∆BAD = ∆ACE\).
b) \(DE = BD + CE\).
-
Bài tập 62 trang 145 SBT Toán 7 Tập 1
Cho tam giác \(ABC.\) Vẽ ở phía ngoài tam giác \(ABC\) các tam giác vuông tại \(A\) là \(ABD, ACE\) có \(AB = AD, AC = AE.\) Kẻ \(AH\) vuông góc với \(BC, DM \) vuông góc với \(AH, EN\) vuông góc với \(AH.\) Chứng minh rằng:
a) \(DM = AH.\)
b) \(MN\) đi qua trung điểm của \(DE\).
-
Bài tập 63 trang 146 SBT Toán 7 Tập 1
Cho tam giác \(ABC, D\) là trung điểm của \(AB.\) Đường thẳng qua \(D\) và song song với \(BC\) cắt \(AC\) ở \(E\), đường thẳng qua \(E\) và song song với \(AB\) cắt \(BC\) ở \(F.\) Chứng minh rằng:
a) \(AD = EF\).
b) \(∆ADE =∆EFC\).
c) \(AE = EC\).
-
Bài tập 64 trang 146 SBT Toán 7 Tập 1
Cho tam giác \(ABC, D\) là trung điểm của \(AB,\) \(E\) là trung điểm của \(AC.\) Vẽ điểm \(F\) sao cho \(E\) là trung điểm của \(DF.\) Chứng minh rằng:
a) \(DB = CF\).
b) \(∆BDC = ∆FCD\).
c) \(DE// BC\) và \(\displaystyle DE = {1 \over 2}BC\)
-
Bài tập 65 trang 146 SBT Toán 7 Tập 1
Cho tam giác \(ABC.\) Trên cạnh \(AB\) lấy các điểm \(D\) và \(E\) sao cho \(AD = BE.\) Qua \(D\) và \(E\), vẽ các đường thẳng song song với \(BC,\) chúng cắt \(AC\) theo thứ tự ở \(M\) và \(N.\) Chứng minh rằng \(DM + EN = BC.\)
Hướng dẫn: Qua \(N,\) kẻ đường thẳng song song với \(AB.\)
-
Bài tập 66 trang 146 SBT Toán 7 Tập 1
Cho tam giác \(ABC\) có \(\widehat A = 60^\circ \). Các tia phân giác của các góc \(B, C\) cắt nhau ở \(I\) và cắt \(AC, AB\) theo thứ tự ở \(D, E.\) Chứng minh rằng \(ID = IE.\)
Hướng dẫn: Kẻ tia phân giác của góc \(BIC\).

.JPG)





