Bài tập 39 trang 209 SGK Toán 12 NC
Giải các phương trình sau trên C:
a.
\(\eqalign{{\left( {z + 3 - i} \right)^2} - 6\left( {z + 3 - i} \right) + 13 = 0}\)
b.
\(\eqalign{\left( {{{iz + 3} \over {z - 2i}}} \right)^2 - 3{{iz + 3} \over {z - 2i}} - 4 = 0;} \)
c.
\({\left( {{z^2} + 1} \right)^2} + {\left( {z + 3} \right)^2} = 0.\)
Hướng dẫn giải chi tiết
a) Đặt w = z + 3 − i ta được phương trình:
\(\begin{array}{*{20}{l}}
\begin{array}{l}
{w^2} - 6w + 13 = 0\\
\Leftrightarrow {(w - 3)^2} = - 4 = 4{i^2}
\end{array}\\
\begin{array}{l}
\Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{w = 3 + 2i}\\
{w = 3 - 2i}
\end{array}} \right.\\
\Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{z + 3 - i = 3 + 2i}\\
{z + 3 - i = 3 - 2i}
\end{array}} \right.\\
\Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{z = 3i}\\
{z = - i}
\end{array}} \right.
\end{array}
\end{array}\)
Vậy S = {−i; 3i}
b) Đặt \(w = \frac{{iz + 3}}{{z - 2i}}\) ta được phương trình:
\({w^2} - 3w - 4 = 0 \Leftrightarrow \left[ \begin{array}{l}
w = - 1\\
w = 4
\end{array} \right.\)
+ Với w = -1 ta có:
\(\frac{{iz + 3}}{{z - 2i}} = - 1 \Leftrightarrow iz + 3 = - z + 2i\)
\(\begin{array}{l}
\Leftrightarrow (i + 1)z = - 3 + 2i\\
\Leftrightarrow z = \frac{{ - 3 + 2i}}{{1 + i}}\\
= \frac{{( - 3 + 2i)(1 - i)}}{2} = \frac{{ - 1 + 5i}}{2}
\end{array}\)
+ Với w = 4 ta có :
\(\frac{{iz + 3}}{{z - 2i}} = 4 \Leftrightarrow (4 - i)z = 3 + 8i\)
\(\begin{array}{l}
\Leftrightarrow z = \frac{{3 + 8i}}{{4 - i}} = \frac{{(3 + 8i)(4 + i)}}{{17}}\\
= \frac{{4 + 35i}}{{17}}
\end{array}\)
Vậy \(S = \left\{ {\frac{{ - 1 + 5i}}{2};\frac{{4 + 35}}{{17}}} \right\}\)
c)
\(\begin{array}{*{20}{l}}
\begin{array}{l}
\begin{array}{*{20}{l}}
{{{({z^2} + 1)}^2} + {{(z + 3)}^2} = {{({z^2} + 1)}^2} - {{[i(z + 3)]}^2}}\\
\end{array}\\
= ({z^2} + 1 + i(z + 3))({z^2} + 1 - i(z + 3)) = 0
\end{array}\\
{ \Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{{z^2} + 1 + i(z + 3) = 0(1)}\\
{{z^2} + 1 - i(z + 3) = 0(2)}
\end{array}} \right.}
\end{array}\)
Phương trình (1) là phương trình bậc hai z2 + iz + 1 + 3i = 0
Δ = −5 − 12i = (2 − 3i)2
Phương trình có hai nghiệm là z1 = 1 − 2i và z2 = −1 + iz
Phương trình (2) là phương trình bậc hai z2 − iz + 1 − 3i = 0
Δ = − 5+ 12i = (2 + 3i)2
Phương trình có hai nghiệm là z3 = 1 + 2i và z4 = −1 − i
Vậy S={1 − 2i; −1 + i; 1 + 2i; −1−i}
-- Mod Toán 12 HỌC247
-

 Mọi người giải giúp em với ạ
Mọi người giải giúp em với ạ Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Tìm tập hợp các điểm M biểu diễn số phức z thỏa |z|<=2
bởi Kim Đoan
 28/04/2020
28/04/2020
 Theo dõi (0) 4 Trả lời
Theo dõi (0) 4 Trả lời -


Tập hợpcác điểm biểu diễn số phức \(w = \dfrac{{5 + iz}}{{1 + z}},\,\,\,|z| = \sqrt 2 \) là một đường tròn có bán kính bằng bao nhiêu?
bởi 12345
 27/04/2020
27/04/2020
Giúp mình câu 3 . Cảm ơn
 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Tìm số phức z thỏa mãn z +2 − 3 i = 3 − 2 i
bởi Lê Thị Oanh
 26/04/2020
26/04/2020
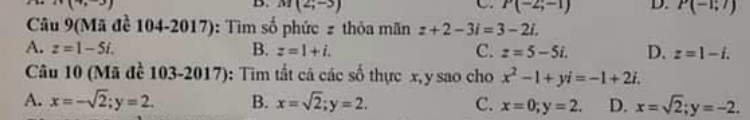 Theo dõi (0) 5 Trả lời
Theo dõi (0) 5 Trả lời -


Tìm giá trị m để số phức z=m-2+(m+1)i là số thuần ảo
Theo dõi (0) 4 Trả lời -


Tìm x, y biết x+2y+(2x-y)i=2x+y+(x+2y)i
bởi Ngọc Trương
 23/04/2020
23/04/2020
Tìm x, y biết x+2y+(2x-y)i=2x+y+(x+2y)i
Theo dõi (0) 2 Trả lời -


Có bao nhiêu số phức z thỏa (1+i)z+z(ngang)
bởi dolly
 14/04/2020
Câu 26 ạ
14/04/2020
Câu 26 ạ Theo dõi (0) 4 Trả lời
Theo dõi (0) 4 Trả lời
Bài tập SGK khác
Bài tập 37 trang 208 SGK Toán 12 NC
Bài tập 38 trang 209 SGK Toán 12 NC
Bài tập 40 trang 209 SGK Toán 12 NC
Bài tập 41 trang 209 SGK Toán 12 NC
Bài tập 42 trang 209 SGK Toán 12 NC
Bài tập 43 trang 210 SGK Toán 12 NC
Bài tập 44 trang 210 SGK Toán 12 NC
Bài tập 45 trang 210 SGK Toán 12 NC
Bài tập 46 trang 210 SGK Toán 12 NC
Bài tập 47 trang 210 SGK Toán 12 NC
Bài tập 48 trang 210 SGK Toán 12 NC
Bài tập 49 trang 210 SGK Toán 12 NC
Bài tập 50 trang 210 SGK Toán 12 NC
Bài tập 51 trang 210 SGK Toán 12 NC
Bài tập 52 trang 210 SGK Toán 12 NC





