Giải bài 6 tr 104 sách GK Toán ĐS & GT lớp 11
Cho hình vuông C1 có cạnh bằng 4. Người ta chia các cạnh của hình vuông thành bốn phần bằng nhau và nối các điểm chia một cách thích hợp để có hình vuông lại làm tiếp tục như trên để được hình vuông C2. Từ hình vuông C2 lại tiếp như trên để được hình vuông C3. Tiếp tục quá trình như trên, ta nhận được dãy các hình vuông \(C_1, C_2, ...,C_n.\) Gọi an là độ dài cạnh của hình vuông Cn. Chứng minh dãy số (an) là một cấp số nhân.
Hướng dẫn giải chi tiết bài 6
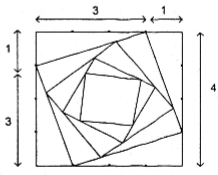
Hình vuông C1 có cạnh a1 = 4. Từ đó ta tính được hình vuông C2 có cạnh \(a_2=\sqrt{1^2+3^2}=\sqrt{10}\), hình vuông C3 có cạnh \(a_3=\frac{5}{2}\), hình vuông C4 có cạnh là \(a_4=\frac{5\sqrt{10}}{8}\)
Từ đó ⇒ \((a_n)\) là cấp số nhân có a1 = 4 và công bội \(q=\frac{\sqrt{10}}{4}.\)
-- Mod Toán 11 HỌC247
Video hướng dẫn giải bài 6 SGK
-


Tỉ lệ tăng dân số của tỉnh X là \(1,4\% \). Biết rằng số dân của tỉnh hiện nay là \(1,8\) triệu người. Hỏi với mức tăng như vậy thì sau 5 năm, 10 năm số dân của tỉnh đó là bao nhiêu?
bởi Nguyen Dat
 23/02/2021
Theo dõi (0) 1 Trả lời
23/02/2021
Theo dõi (0) 1 Trả lời -


Tìm cấp số nhân có sáu số hạng, biết rằng tổng của năm số hạng đầu là \(31\) và tổng của năm số hạng sau là \(62\).
bởi Phan Quân
 24/02/2021
Theo dõi (0) 1 Trả lời
24/02/2021
Theo dõi (0) 1 Trả lời -


Tìm các số hạng của cấp số nhân \((u_n)\) có năm số hạng, biết: \(u_4– u_2= 25\) và \(u_3– u_1= 50\)
bởi thanh duy
 24/02/2021
Theo dõi (0) 1 Trả lời
24/02/2021
Theo dõi (0) 1 Trả lời -


Tìm các số hạng của cấp số nhân \((u_n)\) có năm số hạng, biết: \(u_3= 3\) và \(u_5= 27\).
bởi Khanh Đơn
 23/02/2021
Theo dõi (0) 1 Trả lời
23/02/2021
Theo dõi (0) 1 Trả lời -


Cho cấp số nhân với công bội \(q\). Biết \(u_1= 3, q = -2\). Hỏi số \(192\) là số hạng thứ mấy?
bởi Anh Hà
 23/02/2021
Theo dõi (0) 1 Trả lời
23/02/2021
Theo dõi (0) 1 Trả lời
Bài tập SGK khác
Bài tập 4 trang 104 SGK Đại số & Giải tích 11
Bài tập 5 trang 104 SGK Đại số & Giải tích 11
Bài tập 3.27 trang 131 SBT Toán 11
Bài tập 3.28 trang 131 SBT Toán 11
Bài tập 3.29 trang 131 SBT Toán 11
Bài tập 3.30 trang 131 SBT Toán 11
Bài tập 3.31 trang 131 SBT Toán 11
Bài tập 3.32 trang 131 SBT Toán 11
Bài tập 3.33 trang 131 SBT Toán 11
Bài tập 3.34 trang 132 SBT Toán 11
Bài tập 3.35 trang 132 SBT Toán 11
Bài tập 3.36 trang 132 SBT Toán 11
Bài tập 29 trang 120 SGK Toán 11 NC
Bài tập 30 trang 120 SGK Toán 11 NC
Bài tập 31 trang 121 SGK Toán 11 NC
Bài tập 32 trang 121 SGK Toán 11 NC
Bài tập 33 trang 121 SGK Toán 11 NC
Bài tập 34 trang 121 SGK Toán 11 NC
Bài tập 35 trang 121 SGK Toán 11 NC
Bài tập 36 trang 121 SGK Toán 11 NC
Bài tập 37 trang 121 SGK Toán 11 NC
Bài tập 38 trang 121 SGK Toán 11 NC
Bài tập 39 trang 122 SGK Toán 11 NC
Bài tập 40 trang 122 SGK Toán 11 NC
Bài tập 41 trang 122 SGK Toán 11 NC





