Giải bài 5.4 tr 198 SBT Toán 11
Chứng minh rằng hàm số \(y = |x - 1|\) không có đạo hàm tại , nhưng liên tục tại điểm đó.
Hướng dẫn giải chi tiết
Để chứng minh hàm số không có đạo hàm tại ta chứng minh không tồn tại giới hạn của \(\frac{{f\left( x \right) - f\left( 1 \right)}}{{x - 1}}\)
Ta có: \(\frac{{f\left( x \right) - f\left( 1 \right)}}{{x - 1}} = \frac{{\left| {x - 1} \right|}}{{x - 1}} = \left\{ \begin{array}{l}
1,\,\,\,\,\,x \ge 1\\
- 1,\,\,x < 1
\end{array} \right.\)
Do vậy
\(\begin{array}{l}
\mathop {\lim }\limits_{x \to {1^ - }} \frac{{f\left( x \right) - f\left( 1 \right)}}{{x - 1}} = \mathop {\lim }\limits_{x \to {1^ - }} \left( { - 1} \right) = - 1\\
\mathop {\lim }\limits_{x \to {1^ + }} \frac{{f\left( x \right) - f\left( 1 \right)}}{{x - 1}} = \mathop {\lim }\limits_{x \to {1^ + }} 1 = 1
\end{array}\)
Vì giới hạn hai bên khác nhau nên không tồn tại giới hạn của tỉ số \(\frac{{f\left( x \right) - f\left( 1 \right)}}{{x - 1}}{\rm{khi}}\,x \to 1\)
Vậy hàm số không có đạo hàm tại
Ta có:
\(f\left( x \right) = \left| {x - 1} \right| = \left\{ \begin{array}{l}
x - 1,\,\,\,x \ge 1\\
1 - x,\,\,\,x < 1
\end{array} \right.\)
-- Mod Toán 11 HỌC247
-


Sử dụng định nghĩa, tìm đạo hàm của hàm số sau: \(y = 4{x^2} - 0,6x + 7\)
bởi Nguyen Nhan
 01/03/2021
Theo dõi (0) 1 Trả lời
01/03/2021
Theo dõi (0) 1 Trả lời -

 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


Tính đạo hàm hàm số sau tại các điểm chỉ ra
bởi Trương Hà Anh
 28/02/2021
28/02/2021
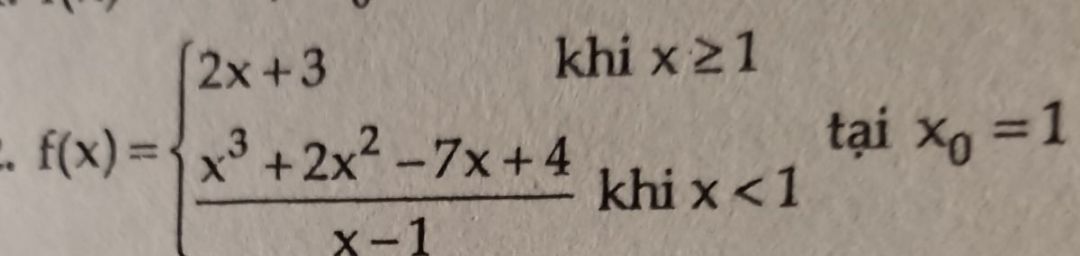 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -

 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời
Bài tập SGK khác
Bài tập 5.2 trang 198 SBT Toán 11
Bài tập 5.3 trang 198 SBT Toán 11
Bài tập 5.5 trang 198 SBT Toán 11
Bài tập 5.6 trang 198 SBT Toán 11
Bài tập 5.7 trang 199 SBT Toán 11
Bài tập 5.8 trang 199 SBT Toán 11
Bài tập 5.9 trang 199 SBT Toán 11
Bài tập 5.10 trang 199 SBT Toán 11
Bài tập 5.11 trang 199 SBT Toán 11
Bài tập 1 trang 192 SGK Toán 11 NC
Bài tập 2 trang 192 SGK Toán 11 NC
Bài tập 3 trang 192 SGK Toán 11 NC
Bài tập 4 trang 192 SGK Toán 11 NC
Bài tập 5 trang 192 SGK Toán 11 NC
Bài tập 6 trang 192 SGK Toán 11 NC
Bài tập 7 trang 192 SGK Toán 11 NC
Bài tập 8 trang 192 SGK Toán 11 NC
Bài tập 9 trang 192 SGK Toán 11 NC
Bài tập 10 trang 195 SGK Toán 11 NC
Bài tập 11 trang 195 SGK Toán 11 NC
Bài tập 12 trang 195 SGK Toán 11 NC
Bài tập 13 trang 195 SGK Toán 11 NC






