Giải bài 5.11 tr 199 SBT Toán 11
Viết phương trình tiếp tuyến của đồ thị hàm số \(y = \sqrt {2x + 1} \) biết hệ số góc của tiếp tuyến bằng \(\frac{1}{3}\)
A. \(y = \frac{x}{2} + \frac{5}{3}\)
B. \(y = \frac{x}{3} - \frac{5}{3}\)
C. \(y = \frac{x}{3} + \frac{5}{3}\)
D. \(y = x - 1\)
Hướng dẫn giải chi tiết
{\rm{\Delta }}y = \sqrt {2\left( {{x_0} + {\rm{\Delta }}x} \right) + 1} - \sqrt {2{x_0} + 1} \\
= \frac{{2\left( {{x_0} + {\rm{\Delta }}x} \right) + 1 - \left( {2{x_0} + 1} \right)}}{{\sqrt {2\left( {{x_0} + {\rm{\Delta }}x} \right) + 1} + \sqrt {2{x_0} + 1} }}\\
= \frac{{2{\rm{\Delta }}x}}{{\sqrt {2\left( {{x_0} + {\rm{\Delta }}x} \right) + 1} + \sqrt {2{x_0} + 1} }}
\end{array}\)
\frac{{\Delta y}}{{\Delta x}} = \frac{{\frac{{2\Delta x}}{{\sqrt {2\left( {{x_0} + \Delta x} \right) + 1} + \sqrt {2{x_0} + 1} }}}}{{\Delta x}}\\
= \frac{2}{{\sqrt {2\left( {{x_0} + \Delta x} \right) + 1} + \sqrt {2{x_0} + 1} }}\\
\Rightarrow y'\left( {{x_0}} \right) = \mathop {\lim }\limits_{\Delta x \to 0} \frac{2}{{\sqrt {2\left( {{x_0} + \Delta x} \right) + 1} + \sqrt {2{x_0} + 1} }} = \frac{1}{{\sqrt {2{x_0} + 1} }}
\end{array}\)
-- Mod Toán 11 HỌC247
-


Chứng minh phương trình x^5-3x=1 có ít nhất 2 nghiệm thực
bởi Mỹ Tiên
 16/02/2021
Chứng minh phương trình x^5-3x=1 có ít nhất 2 nghiệm thựcTheo dõi (0) 0 Trả lời
16/02/2021
Chứng minh phương trình x^5-3x=1 có ít nhất 2 nghiệm thựcTheo dõi (0) 0 Trả lời -


Tìm điều kiện của a, b, c để mọi tiếp tuyến của (C) đều có hệ số góc âm?
bởi Nguyễn Huyền
 08/07/2020
08/07/2020
Câu 45
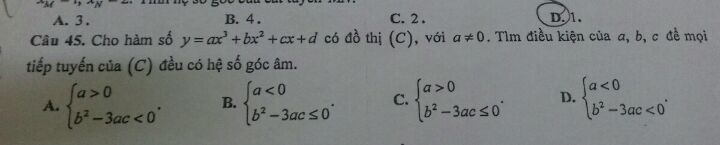 Theo dõi (0) 2 Trả lời
Theo dõi (0) 2 Trả lời -


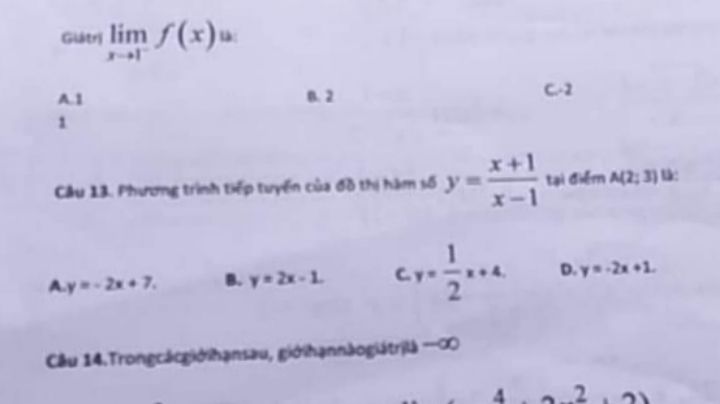 Theo dõi (0) 2 Trả lời
Theo dõi (0) 2 Trả lời -


Tính đạo hàm f'(x) tại điểm x=0?
bởi Hân
 25/06/2020
25/06/2020
 Theo dõi (0) 3 Trả lời
Theo dõi (0) 3 Trả lời
Bài tập SGK khác
Bài tập 5.9 trang 199 SBT Toán 11
Bài tập 5.10 trang 199 SBT Toán 11
Bài tập 1 trang 192 SGK Toán 11 NC
Bài tập 2 trang 192 SGK Toán 11 NC
Bài tập 3 trang 192 SGK Toán 11 NC
Bài tập 4 trang 192 SGK Toán 11 NC
Bài tập 5 trang 192 SGK Toán 11 NC
Bài tập 6 trang 192 SGK Toán 11 NC
Bài tập 7 trang 192 SGK Toán 11 NC
Bài tập 8 trang 192 SGK Toán 11 NC
Bài tập 9 trang 192 SGK Toán 11 NC
Bài tập 10 trang 195 SGK Toán 11 NC
Bài tập 11 trang 195 SGK Toán 11 NC
Bài tập 12 trang 195 SGK Toán 11 NC
Bài tập 13 trang 195 SGK Toán 11 NC






