Qua bài viết này, chúng ta sẽ tìm hiểu và khám phá sâu hơn về Phương trình lượng giác cơ bản chương trình Toán 11 Chân trời sáng tạo, các quy tắc và phép biến đổi để giải các phương trình này, cùng với một số ứng dụng thực tiễn trong đời sống và khoa học.
Tóm tắt lý thuyết
1.1. Phương trình tương đương
|
- Hai phương trình được gọi là tương đương khi chúng có cùng tập nghiệm. |
1.2. Phương trình sin x = m
|
Xét phương trình sin x = m. - Nếu |m| > 1 thì phương trình vô nghiệm. - Nếu |m| ≤ 1 thì phương trình có nghiệm: \(\left[ \begin{array}{l} x = \alpha + k2\pi \\ x = \pi - \alpha + k2\pi \end{array} \right. (k\in Z)\) với \(\alpha \in \left[ { - \frac{\pi }{2};\frac{\pi }{2}} \right]\) sao cho sin \(\alpha \) = m. |
.PNG)
Chú ý
- Một số trường hợp đặc biệt.
|
\(\sin x = 0 \Leftrightarrow x = k\pi ,(k \in Z)\\ \sin x = 1 \Leftrightarrow x = \frac{\pi }{2} + k2\pi ,(k \in Z)\\ \sin x = - 1 \Leftrightarrow x = - \frac{\pi }{2} + k2\pi ,(k \in Z)\) |
- Hơn nữa ta có:
| \(\begin{array}{l} \sin u = \sin v \\ \Leftrightarrow {\rm{ }}\left[ \begin{array}{l} u = v + k2\pi\\ u = \pi - v + k2\pi \end{array} \right.(k \in Z) \end{array}\) |
- Nếu số đo của góc \(\alpha \) được cho bằng đơn vị độ thì
| \(\begin{array}{l} \sin x = \sin \alpha \\ \Leftrightarrow {\rm{ }}\left[ \begin{array}{l} x = {\alpha ^0} + k{360^0}\\ x = 180 ^0 - {\alpha ^0} + k{360^0} \end{array} \right.(k \in Z) \end{array}\) |
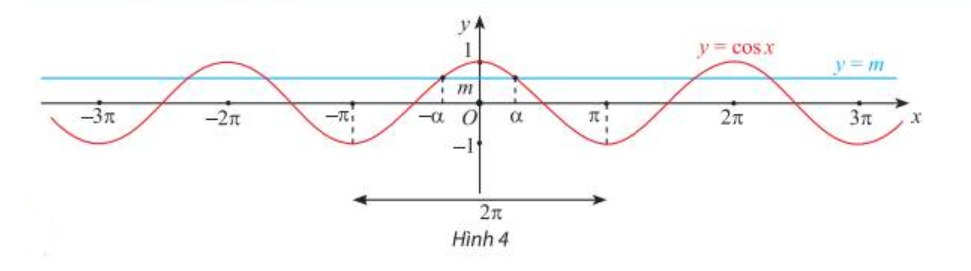
1.3. Phương trình cos x = m
|
Xét phương trình cos x = m. - Nếu |m| > 1 thì phương trình vô nghiệm. - Nếu |m| ≤ 1 thì phương trình có nghiệm: \(\left[ \begin{array}{l} x = \alpha + k2\pi \\ x = - \alpha + k2\pi \end{array} \right. (k\in Z)\) với \(\alpha \in \left[ {0;{\pi }} \right]\) sao cho cos \(\alpha \) = m. |
Chú ý
- Một số trường hợp đặc biệt.
|
\(\cos x = 0 \Leftrightarrow x = k\pi ,(k \in Z)\\ \cos x = 1 \Leftrightarrow x = k2\pi ,(k \in Z)\\ \cos x = - 1 \Leftrightarrow x = {\pi } + k2\pi ,(k \in Z)\) |
- Hơn nữa ta có:
| \(\begin{array}{l} \cos u = \cos v \\ \Leftrightarrow {\rm{ }}\left[ \begin{array}{l} u = v + k2\pi\\ u = - v + k2\pi \end{array} \right.(k \in Z) \end{array}\) |
- Nếu số đo của góc \(\alpha \) được cho bằng đơn vị độ thì
| \(\begin{array}{l} \cos x = \cos \alpha \\ \Leftrightarrow {\rm{ }}\left[ \begin{array}{l} x = {\alpha ^0} + k{360^0}\\ x = -{\alpha ^0} + k{360^0} \end{array} \right.(k \in Z) \end{array}\) |
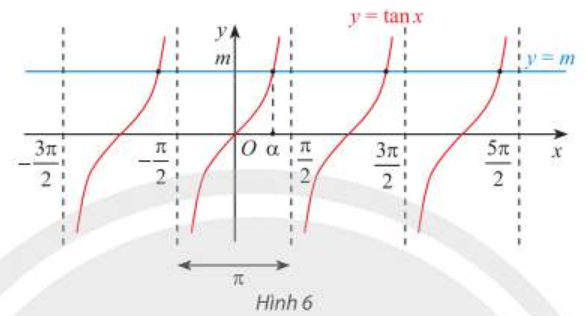
1.4. Phương trình tan x = m
|
- Với mọi số thực m, phương trình tan x = m có nghiệm \(x = \alpha + k\pi \quad (k\in Z)\) với \(\alpha \in \left( {-{\pi \over 2};{\pi \over 2}} \right)\) sao cho tan \(\alpha \) = m. |
Chú ý
- Nếu số đo của góc \(\alpha \) được cho bằng đơn vị độ thì
| \( \tan x = \tan \alpha \Leftrightarrow {\rm{ }} x = {\alpha ^0} + k{180^0}(k \in Z) \) |
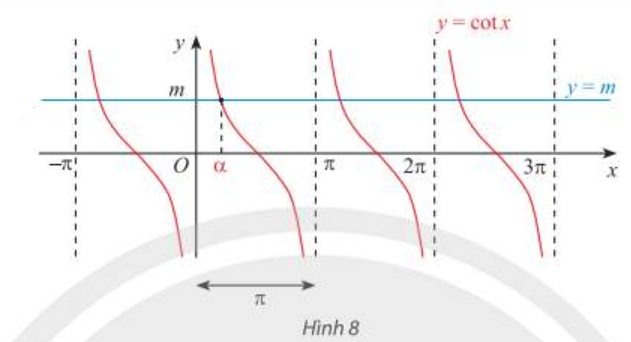
1.5. Phương trình cot x = m
|
- Với mọi số thực m, phương trình cot x = m có nghiệm \(x = \alpha + k\pi \quad (k\in Z)\) với \(\alpha \in \left( {0;{\pi }} \right)\) sao cho cot \(\alpha \) = m. |
Chú ý
- Nếu số đo của góc \(\alpha \) được cho bằng đơn vị độ thì
| \( \cot x = \cot \alpha \Leftrightarrow {\rm{ }} x = {\alpha ^0} + k{180^0}(k \in Z) \) |
Bài tập minh họa
Câu 1: Giải các phương trình sau:
\(a)\,\,\sin x=\sin \frac{\pi }{12}\)
\(b)\,\,\sin 2x=-\sin {{36}^{0}}\)
\(c)\,\,\sin 3x=\frac{1}{2}\)
\(d)\,\,\sin x=\frac{2}{3}\)
Hướng dẫn giải
\(a)\,\,\sin x=\sin \frac{\pi }{12}\\\Leftrightarrow \left[ \begin{align} & x=\frac{\pi }{12}+k2\pi \\ & x=\pi -\frac{\pi }{12}+k2\pi \\ \end{align} \right.\)
\(\Leftrightarrow \left[ \begin{align} & x=\frac{\pi }{12}+k2\pi \\ & x=\frac{11\pi }{12}+k2\pi \\ \end{align} \right.\left( k\in \mathbb{Z} \right)\)
\(b)\,\,\sin 2x=-\sin {{36}^{0}}\\ \Leftrightarrow \sin 2x=\sin \left( -{{36}^{0}} \right) \\ \Leftrightarrow \left[ \begin{align} & 2x=-{{36}^{0}}+k{{360}^{0}} \\ & 2x={{180}^{0}}-\left( -{{36}^{0}} \right)+k{{360}^{0}} \\ \end{align} \right. \)
\(\Leftrightarrow \left[ \begin{align} & 2x=-{{36}^{0}}+k{{360}^{0}} \\ & 2x={{216}^{0}}+k{{360}^{0}} \\ \end{align} \right.\)
\(\Leftrightarrow \left[ \begin{align} & x=-{{18}^{0}}+k{{180}^{0}} \\ & x={{108}^{0}}+k{{180}^{0}} \\ \end{align} \right.\left( k\in \mathbb{Z} \right)\)
\(c)\,\,\sin 3x=\frac{1}{2}\\\Leftrightarrow \sin 3x=\sin \frac{\pi }{6}\\\Leftrightarrow \left[ \begin{align} & 3x=\frac{\pi }{6}+k2\pi \\ & 3x=\frac{5\pi }{6}+k2\pi \\ \end{align} \right.\)
\(\Leftrightarrow \left[ \begin{align} & x=\frac{\pi }{18}+k\frac{2\pi }{3} \\ & x=\frac{5\pi }{18}+k\frac{2\pi }{3} \\ \end{align} \right.\left( k\in \mathbb{Z} \right)\)
\(d)\,\,\sin x=\frac{2}{3}\\\Leftrightarrow \left[ \begin{align} & x=\arcsin \frac{2}{3}+k2\pi \\ & x=\pi -\arcsin \frac{2}{3}+k2\pi \\ \end{align} \right.\left( k\in \mathbb{Z} \right)\)
Luyện tập Bài 5 Toán 11 Chân Trời Sáng Tạo
Học xong bài học này, em có thể:
- Nhận biết các khái niệm về phương trình tương đương, phương trình lượng giác.
- Sử dụng máy tính cầm tay để giải phương trình lượng giác.
3.1. Trắc nghiệm Bài 5 Toán 11 Chân Trời Sáng Tạo
Các em có thể hệ thống lại nội dung kiến thức đã học được thông qua bài kiểm tra Trắc nghiệm Toán 11 Chân trời sáng tạo Chương 1 Bài 5 cực hay có đáp án và lời giải chi tiết.
-
- A. \(2 + k\pi \)
- B. \(k\pi \)
- C. \(\arctan 2 + k\pi \)
- D. \(\arctan \dfrac{1}{2} + k\pi \)
-
- A. \(\sin x = - \dfrac{1}{2}\)
- B. \(\cot x = - \dfrac{{\sqrt 3 }}{3}\)
- C. \(\tan x = \sqrt 3 \)
- D. \(\cos x = - \dfrac{1}{2}\)
-
- A. \(\dfrac{\pi }{3} + k\pi \)
- B. \(\dfrac{\pi }{6} + k\pi \)
- C. \(\dfrac{{5\pi }}{6} + k\pi \)
- D. \( - \dfrac{\pi }{6} + k2\pi \)
Câu 4-10: Mời các em đăng nhập xem tiếp nội dung và thi thử Online để củng cố kiến thức về bài học này nhé!
3.2. Bài tập SGK Bài 5 Toán 11 Chân Trời Sáng Tạo
Các em có thể xem thêm phần hướng dẫn Giải bài tập Toán 11 Chân trời sáng tạo Chương 1 Bài 5 để giúp các em nắm vững bài học và các phương pháp giải bài tập.
Hoạt động khởi động trang 34 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Hoạt động khám phá 1 trang 34 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Thực hành 1 trang 34 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Hoạt động khám phá 2 trang 35 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Thực hành 2 trang 36 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Hoạt động khám phá 3 trang 36 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Thực hành 3 trang 37 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Hoạt động khám phá 4 trang 37 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Thực hành 4 trang 38 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Hoạt động khám phá 5 trang 38 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Thực hành 5 trang 39 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Thực hành 6 trang 40 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Vận dụng trang 40 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Giải Bài 1 trang 40 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Giải Bài 2 trang 40 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Giải Bài 3 trang 41 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Giải Bài 4 trang 41 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Giải Bài 5 trang 41 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Giải Bài 6 trang 41 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Giải Bài 7 trang 41 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Bài tập 1 trang 30 SBT Toán 11 Tập 1 Chân trời sáng tạo - CTST
Bài tập 2 trang 31 SBT Toán 11 Tập 1 Chân trời sáng tạo - CTST
Bài tập 3 trang 31 SBT Toán 11 Tập 1 Chân trời sáng tạo - CTST
Bài tập 4 trang 31 SBT Toán 11 Tập 1 Chân trời sáng tạo - CTST
Bài tập 5 trang 31 SBT Toán 11 Tập 1 Chân trời sáng tạo - CTST
Bài tập 6 trang 31 SBT Toán 11 Tập 1 Chân trời sáng tạo - CTST
Bài tập 7 trang 31 SBT Toán 11 Tập 1 Chân trời sáng tạo - CTST
Bài tập 8 trang 31 SBT Toán 11 Tập 1 Chân trời sáng tạo - CTST
Bài tập 9 trang 31 SBT Toán 11 Tập 1 Chân trời sáng tạo - CTST
Bài tập 10 trang 32 SBT Toán 11 Tập 1 Chân trời sáng tạo - CTST
Hỏi đáp Bài 5 Toán 11 Chân Trời Sáng Tạo
Trong quá trình học tập nếu có thắc mắc hay cần trợ giúp gì thì các em hãy comment ở mục Hỏi đáp, Cộng đồng Toán học HOC247 sẽ hỗ trợ cho các em một cách nhanh chóng!
Chúc các em học tập tốt và luôn đạt thành tích cao trong học tập!
-- Mod Toán Học 11 HỌC247
