Bài học Góc lượng giác Toán 11 Chân trời sáng tạo là bài đầu tiên trong phần lượng giác, một phần quan trọng trong toán học. Do đó, các em cần nắm vững nội dung của bài học này để có thể dễ dàng tiếp cận kiến thức những bài tiếp theo. Trong bài này, chúng ta sẽ đi tìm hiểu thế nào là góc lượng giác, đơn vị radian và đường tròn lượng giác. Chúc các em học tập thật vui vẻ!
Tóm tắt lý thuyết
1.1. Góc lượng giác
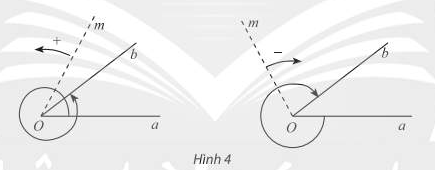
Khi xét chuyển động quay của một tia Om ta quy ước: Chiều quay ngược với chiều quay của kim đồng hồ là chiều dương, chiều quay cùng chiều kim đồng hồ là chiều âm.
|
Cho hai tia Oa, Ob. - Nếu một tia Om quay quanh gốc O của nó theo một chiều cố định bắt đầu từ vị trí tia Oa và dừng ở vị trí tia Ob thì ta nói tia Om quét một góc lượng giác có tia đầu Oa, tia cuối Ob, kí hiệu (Oa, Ob). - Khi tia Om quay một góc \(\alpha\), ta nói số đo của góc lượng giác (Oa, Ob) bằng \(\alpha\), kí hiệu sđ(Oa, Ob) = \(\alpha\). |
Chú ý: Với hai tia Oa và Ob cho trước, có vô số góc lượng giác tia đầu Oa và tia cuối Ob.
Ta dùng chung kí hiệu (Oa, Ob) cho tất cả các góc lượng giác này.
Nhận xét: Số đo của các góc lượng giác có cùng tia đầu Oa và tia cuối Ob sai khác nhau một bội nguyên của 360° nên có công thức tổng quát là:
sđ(Oa , Ob) = \(\alpha ^0\) +k 360\(^0\) (k ∈ Z)
với \(\alpha ^0\) là số đo của một góc lượng giác bất kì có tia đầu Oa và tia cuối Ob.
Ta thừa nhận hệ thức sau: gọi là Hệ thức Chasles:
|
Với ba tia Oa, Ob, Oc bất kì, ta có sđ(Oa, Ob) + sđ(Ob, Oc) = sđ(Oa,Oc) + k360° (k ∈ Z). |
1.2. Đơn vị radian
|
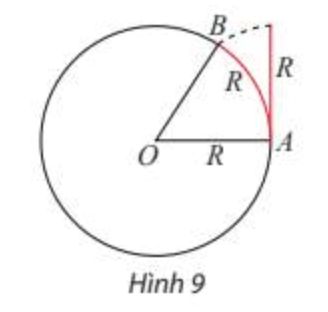
Trên đường tròn bán kính R tuỳ ý, góc ở tâm chắn một cung có độ dài đúng bằng R được gọi là một góc có số đo 1 radian (đọc là 1 ra-đi-an, viết tắt là 1 rad). |
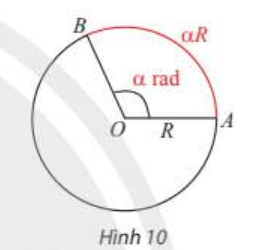
Trên đường tròn bán kính R, một góc ở tâm có số đo \(\alpha\) rad thì chắn một cung có độ dài \(\alpha\)R (Hình 10).
Công thức chuyển đổi số đo góc từ đơn vị radian sang độ và ngược lại:
|
\(a\)° = \(\pi a\over 180\) rad và \(\alpha\) rad = \({180 \alpha\over \pi}^°\) |
Chú ý:
+ Khi viết số đo của một góc theo đơn vị radian, người ta thường không viết chữ rad sau số đo.
+ Với đơn vị radian, công thức số đo tổng quát của góc lượng giác (Oa, Ob) là
(Оa, Ob) = \(\alpha\) + k2π (k ∈ Z).
trong đó \(\alpha\) là số đo theo radian của một góc lượng giác bất kẻ có tia đầu Oa và tia cuối Ob.
Lưu ý: không được viết \(\alpha\) + k360° hay a° +k2π (vì không cùng đơn vị đo).
1.3. Đường tròn lượng giác
|
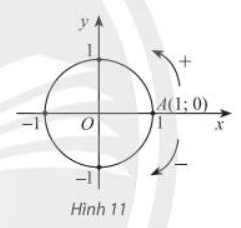
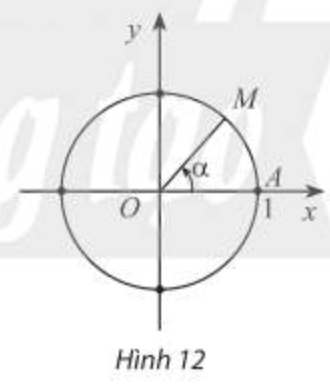
Trong mặt phẳng toạ độ Oxy, cho đường tròn tâm O bán kính bằng 1. Trên đường tròn này, chọn điểm A(1;0) làm gốc, chiều dương là chiều ngược chiều kim đồng hồ và chiều âm là chiều cùng chiều kim đồng hồ. Đường tròn cùng với gốc và chiều như trên được gọi là đường tròn lượng giác. |
Cho số đo góc \(\alpha\) bất kì. Trên đường tròn lượng giác, ta xác định được duy nhất một điểm M sao cho số do góc lượng giác (OA, OM) bằng \(\alpha\) (Hình 12). Khi đó điểm M được gọi là điểm biểu diễn của góc có số đo ở trên đường tròn lượng giác.
Bài tập minh họa
Câu 1: Đổi số đo của góc sang đơn vị radian
Áp dụng công thức với tính bằng radian, a tính bằng độ
Ta có
Câu 2: Một đường tròn có đường kính bằng 20cm. Tính độ dài của cung trên đường tròn có số đo 350 (lấy 2 chữ số thập phân).
Hướng dẫn giải
Cung có số đo 350 thì số đo radian là
Bán kính đường tròn
Suy ra
Luyện tập Bài 1 Toán 11 Chân Trời Sáng Tạo
Học xong bài học này, em có thể:
- Nhận biết khái niệm góc lượng giác.
- Biểu diễn được các góc lượng giác trên đường tròn lượng giác.
3.1. Trắc nghiệm Bài 1 Toán 11 Chân Trời Sáng Tạo
Các em có thể hệ thống lại nội dung kiến thức đã học được thông qua bài kiểm tra Trắc nghiệm Toán 11 Chân trời sáng tạo Chương 1 Bài 1 cực hay có đáp án và lời giải chi tiết.
-
- A. 1
- B. 3
- C. 2
- D. 0,5
-
- A. \(360{}^\circ \) và \(2\pi \)
- B. \(360{}^\circ \) và \(\pi \)
- C. \(\frac{1080{}^\circ }{\pi }\) và 6
- D. \(1080{}^\circ \) và \(6\pi \)
-
- A. \(\frac{5\pi }{6}\)
- B. \(\frac{\pi }{6}\)
- C. \(\frac{-13\pi }{6}\)
- D. \(\frac{-11\pi }{6}\)
Câu 4-10: Mời các em đăng nhập xem tiếp nội dung và thi thử Online để củng cố kiến thức về bài học này nhé!
3.2. Bài tập SGK Bài 1 Toán 11 Chân Trời Sáng Tạo
Các em có thể xem thêm phần hướng dẫn Giải bài tập Toán 11 Chân trời sáng tạo Chương 1 Bài 1 để giúp các em nắm vững bài học và các phương pháp giải bài tập.
Hoạt động khởi động trang 7 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Hoạt động khám phá 1 trang 7 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Thực hành 1 trang 9 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Vận dụng 1 trang 9 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Hoạt động khám phá 2 trang 9 SGK Toán 11 Chân trời sáng tạo tập 1
Vận dụng 2 trang 9 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Hoạt động khám phá 3 trang 10 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Thực hành 2 trang 11 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Hoạt động khám phá 4 trang 11 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Thực hành 3 trang 12 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Giải Bài 1 trang 12 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Giải Bài 2 trang 12 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Giải Bài 3 trang 12 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Giải Bài 4 trang 12 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Giải Bài 5 trang 12 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Giải Bài 6 trang 12 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Giải Bài 7 trang 13 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Giải Bài 8 trang 13 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Giải Bài 9 trang 13 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Bài tập 1 trang 8 SBT Toán 11 Tập 1 Chân trời sáng tạo - CTST
Bài tập 2 trang 8 SBT Toán 11 Tập 1 Chân trời sáng tạo - CTST
Bài tập 3 trang 8 SBT Toán 11 Tập 1 Chân trời sáng tạo - CTST
Bài tập 4 trang 9 SBT Toán 11 Tập 1 Chân trời sáng tạo - CTST
Bài tập 5 trang 9 SBT Toán 11 Tập 1 Chân trời sáng tạo - CTST
Bài tập 6 trang 9 SBT Toán 11 Tập 1 Chân trời sáng tạo - CTST
Bài tập 7 trang 9 SBT Toán 11 Tập 1 Chân trời sáng tạo - CTST
Bài tập 8 trang 9 SBT Toán 11 Tập 1 Chân trời sáng tạo - CTST
Bài tập 9 trang 9 SBT Toán 11 Tập 1 Chân trời sáng tạo - CTST
Bài tập 10 trang 9 SBT Toán 11 Tập 1 Chân trời sáng tạo - CTST
Bài tập 11 trang 10 SBT Toán 11 Tập 1 Chân trời sáng tạo - CTST
Bài tập 12 trang 10 SBT Toán 11 Tập 1 Chân trời sáng tạo - CTST
Bài tập 13 trang 10 SBT Toán 11 Tập 1 Chân trời sáng tạo - CTST
Hỏi đáp Bài 1 Toán 11 Chân Trời Sáng Tạo
Trong quá trình học tập nếu có thắc mắc hay cần trợ giúp gì thì các em hãy comment ở mục Hỏi đáp, Cộng đồng Toán học HOC247 sẽ hỗ trợ cho các em một cách nhanh chóng!
Chúc các em học tập tốt và luôn đạt thành tích cao trong học tập!
-- Mod Toán Học 11 HỌC247