Giải bài 3.15 tr 11 sách BT Lý lớp 12
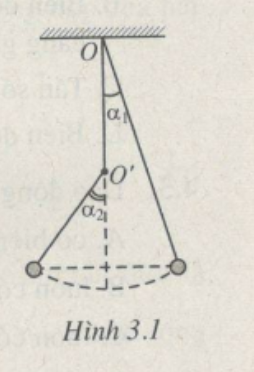
Một con lắc đơn dài 2,0 m. Phía dưới điểm treo O trên phương thẳng đứng có một chiếc đinh đóng chắc vào điểm O' cách O một đoạn OO' = 0,5 m, sao cho con lắc vấp vào đinh khi dao động (H.3.1). Kéo con lắc lệch khỏi phương thẳng đứng một góc α1 = 7o rồi thả không vận tốc đầu. Bỏ qua ma sát. Hãy tính :
a) Biên độ góc của con lắc ở hai bên vị trí cân bằng.
b) Chu kì dao động của con lắc. Lấy g = 9,8 m/s2. Hình 3.1
Hướng dẫn giải chi tiết
a) Biên độ góc của con lắc ở hai bên vị trí cân bằng.
Theo định luật bảo toàn năng lượng ta suy ra hai vị trí biên phải ở cùng 1 độ cao:
\(\begin{array}{*{20}{l}} {{h_A}\; = {h_B}}\\ {l\left( {1 - cos{\alpha _1}} \right) = \frac{{3l}}{4}.\left( {1 - cos{\alpha _2}} \right)}\\ { \Rightarrow {\rm{ }}cos{\alpha _2}\; = \frac{1}{3}{\rm{ }}.\left( {4cos{\alpha _1}\; - 1} \right) = \frac{1}{3}.\left( {4cos{7^o}\; - {\rm{ }}1} \right){\rm{ }} \approx {\rm{ }}0,99}\\ { \Rightarrow {\rm{ }}{\alpha _2}\; = 8,{1^o}} \end{array}\)
b) Chu kì dao động của con lắc
\(\begin{array}{l} T = \frac{{{T_1}\; + {\rm{ }}{T_2}}}{2}\\ {T_1} = 2\pi \sqrt {\frac{l}{g}} ;{T_2} = 2\pi \sqrt {\frac{{3l}}{{4g}}} = 2\pi \sqrt {\frac{l}{g}} .\frac{{\sqrt 3 }}{2}\\ \Rightarrow T = \pi \sqrt {\frac{l}{g}} .\left( {1 + \frac{{\sqrt 3 }}{2}} \right) = \pi \sqrt {\frac{2}{{9,8}}} .\left( {1 + \frac{{\sqrt 3 }}{2}} \right)\\ \Rightarrow T = 2,65s \end{array}\)
-- Mod Vật Lý 12 HỌC247
-


Tìm tần số dao động của con lắc đơn biết rằng mỗi phút con lắc thực hiện 360 dao động
bởi Anh Nguyễn
 14/09/2018
14/09/2018
Dao động của con lắc đơn là 1 dao động tuần hoàn.Biết rằng mỗi phút con lắc thực hiện 360 dao động.Tìm tần số dao động của con lắc?
Theo dõi (0) 1 Trả lời -


Nói rõ sự chuyển hóa năng lượng con lắc đơn trong quá trình di chuyển ?
bởi Nguyễn Thủy Tiên
 31/01/2019
31/01/2019
Con lăc đơn được treo trên 1 trần nhà như hình vẽ bên, lấy tay kéo con lắc tới C rồi buông nhẹ.
a) Nhận xét về vị trí cđ của con lắc ? Sau 1 tg dài con lắc ở vị trí nào ?
b) Nói rõ sự chuyển hóa năng lượng con lắc trong quá trình di chuyển ?
@Thành Đạt Mai Nguyễn @Phương An @Đức Minh... và các bạn khác nữa, giúp vs
Theo dõi (0) 1 Trả lời -


Tại sao mặt phẳng nghiêng lại giảm lực kéo ?
bởi Dương Quá
 28/02/2019
28/02/2019
các bạn ơi ! tại sao mặt phẵng ngiêng lại giảm lực kéo vậy ?
giúp mình đi
Theo dõi (0) 1 Trả lời -


Tìm vị trí li độ góc của 1 con lắc đơn DĐĐH tại nơi có động năng bằng n lần thế năng
bởi Hoai Hoai
 14/09/2018
14/09/2018
1 com lắc đơn DĐ ĐH với biên độ góc \(\alpha_0\).con lắc có động năng bằng n lần thế năng tại vị trí có li độ góc
A.\(\alpha=\dfrac{\alpha_0}{n}\)
B.\(\alpha=\dfrac{\alpha_0}{n+1}\)
C.\(\alpha=\pm\dfrac{\alpha_0}{\sqrt{n+1}}\)
D.\(\alpha=\pm\dfrac{\alpha_0}{n+1}\)
Theo dõi (0) 1 Trả lời -


Tính biên độ của con lắc đơn có chiều dài l=100cm khi dao động với tần số ngoại lực f1=0,5Hz, f2=0,5Hz, f3=0,75Hz
bởi Mai Bảo Khánh
 18/09/2018
18/09/2018
Một con lắc đơn có chiều dài l=100cm treo tại nơi có gia tốc rơi tự do g=π^2 tác dụng một ngoại lực t tuần hoàn lên con lắc có bien độ không đoi. Khi tan số ngoai lực f1=0,5Hz f2=0,5Hz f3=0,75Hz con lắc sẽ dao động với các biên độ nhỏ lần lượt la A1 A2 A3
Theo dõi (0) 1 Trả lời -


Tính giá trị α0 của 1con lắc đơn đang DĐĐH với biên độ góc α0 tại nơi có gia tốc trọng trường là g
bởi Đào Lê Hương Quỳnh
 14/09/2018
14/09/2018
Một con lắc đơn đang dao động điều hòa với biên độ góc α0 tại nơi có gia tốc trọng trường la g.biết lực căng dây lớn nhất bằng 1,02 lần lực căng dây nhỏ nhất.giá trị của α0 là ?
Theo dõi (0) 1 Trả lời -


Tính chiều dài ban đầu của con lắc đơn trong khoảng thời gian Δt nó thực hiện được 6 DĐĐH
bởi Lê Văn Duyệt
 14/09/2018
14/09/2018
Một con lắc đơn có chiều dài l, trong khoảng thời gian Δt nó thực hiện được 6 dao động điều hòa. Người ta giảm bớt độ dài của nó 16(cm), cũng trong khoảng thời gian Δt như trước nó thực hiện được 10 dao động. Chiều dài bam đầu của con lắc là:
Theo dõi (0) 1 Trả lời -


1/Hai nguồn sóng AB cách nhau 1,1m dao động chạm nhẹ trên mặt chất lỏng, cùng tần số 100Hz, cùng pha theo phương vuông góc với mặt chất lỏng vận tốc truyền sóng 20m/s. Số điểm không dao động trên đoạn AB là:
A.15 điểm
B.11 điểm
C.10 điểm
D.20 điểm
2/Một con lắc đơn dao động điều hòa tại địa điểm A.Nếu đem con lắc đến địa điểm B, biết rằng chiều dài con lắc ko đổi còn gia tốc trọng trường tại B bằng 81% gia tốc trọng trường tại A. So với tần số dao động của con lắc tại A, tần số dao động của con lắc tại B là:
A.tăng 10%
B. giảm 9%
C.tằng 9%
D. giảm 10%
3/ Chọn phát biểu đúng khi nói về năng lượng của vật dao động điều hòa:
A. khi đi từ vị trí cân bằng ra biên thì động năng của vật năng
B. khi đi từ vj trí biên về vị trí cân bằng thì thế năng của vật năng
C. khi đi từ vị trí cân bằng ra biên thì cơ năng của vật tăng dần
D.ở vị trí cân bằng thì động năng của vật đạt giá trị cực đại và bằng cơ năng
4/Một chất điểm dao động điều hòa trên trục Ox(với O là VTCB) có vận tốc bằng nửa
giá trị cực đại tại hai thời điểm liên tiếp t 1 = 2,8s và t 2 = 3,6s; tốc độ trung bình trong khoảng
thời gian đó là (10 căn 3)/pi
. Tốc độ dao động cực đại của chất điểm là
A. 15cm/s B. 10 / cm s C. 8cm/s D. 20cm/sTheo dõi (0) 9 Trả lời -


Tính chu kỳ dao động con lắc đơn dao động trong điện trường vectơ E thẳng đứng chiều hướng xuống
bởi Lê Minh
 14/09/2018
Một con lắc đơn chiều dài l. Khối lượng m điện tích q dương. QE nhỏ hơn mg. Con lắc dao động chu kỳ T0 khi không có điện trường. Cho con lắc dao độg trong điện trường vectơ E thẳng đứng chiều hướng xuốg. Hỏi chu kỳ dao động con lắcTheo dõi (0) 1 Trả lời
14/09/2018
Một con lắc đơn chiều dài l. Khối lượng m điện tích q dương. QE nhỏ hơn mg. Con lắc dao động chu kỳ T0 khi không có điện trường. Cho con lắc dao độg trong điện trường vectơ E thẳng đứng chiều hướng xuốg. Hỏi chu kỳ dao động con lắcTheo dõi (0) 1 Trả lời -


Tính biên độ góc mà con lắc đạt được sau khi vướng vào 1 chiếc đinh nằm trên đường thẳng đứng cách điểm treo con lắc 1 đoạn l/2
bởi Trịnh Lan Trinh
 14/09/2018
14/09/2018
một con lắc đơn có chiều dài l. Kéo con lắc lệch khỏi vị trí cân bằng một góc \anpha_{0}= 30 độ rồi thả nhẹ cho dao động. Khi đi qua VTCB dây treo bị vướng vào 1 chiếc đinh nằm trên đường thẳng đứng cách điểm treo con lắc 1 đoạn l/2. Tính biên độ góc beta mà con lắc đạt được sau khi vướng đinh?
Theo dõi (0) 1 Trả lời -


Con lắc đơn dài 1m. Kéo khổ vtcb góc nhỏ. Khi qua vtcb bị vướng đinh. Đinh dưới điểm treo 36cm. Hỏi chu kỳ dao con lắc
Theo dõi (0) 1 Trả lời -


Tính chu kì dao động của con lắc đơn thứ 3 có chiều dài bằng tích chiều dài của 2 con lắc l1 và l2 có chu kì dao động riêng là T1 và T2
bởi Nguyễn Hiền
 14/09/2018
14/09/2018
tại cùng một nơi có gia tốc trọng trường g,hai con lắc đơn dài l1 và l2 có chu kì dao động riêng là T1 và T2,chu kì dao động của con lắc đơn thứ 3 có chiều dài bằng tích chiều dài của 2 con lắc nói trên là:
Theo dõi (0) 1 Trả lời -


Một con lắc đơn dao động tại điểm A có nhiệt độ 250C và tại địa điểm B có nhiệt độ 100C với cùng một chu kì thì gia tốc trọng trường tại B tăng hay giảm bao nhiêu %
bởi Tieu Dong
 14/09/2018
14/09/2018
1/ Một con lắc đơn dao động tại điểm A có nhiệt độ 250C và tại địa điểm B có nhiệt độ 100C với cùng một chu kì. Hỏi so với gia tốc trong trường tại A thì gia tốc trọng trường tại B tăng hay giảm bao nhiêu %? Cho hệ số nở dài của dây treo con lắc là = 4.10-5K -1 . A. tăng 0,06% B. giảm 0,06% C. tăng 0,6% D. giảm 0,6%
2/ Một con lắc đơn có dây treo bằng kim loại và có hệ số nở dài = 2.10-5K -1 ở mặt đất nhiệt độ 300C. Đưa lên độ cao h, ở đó nhiệt độ 100C thì thấy trong một ngày đêm con lắc chạy nhanh 4,32s. Cho bán kính Trái Đất R = 6500km. Độ cao h là:
A. 0,48km B. 1,6km C. 0,64km D. 0,96km
3/Hai con lắc đơn giống hệt nhau, các quả cầu dao động có kích thức nhỏ làm bằng chất có khối lượng riêng D =8450 kg/m3 . Dùng các con lắc nói trên để điều khiển các đồng hồ quả lắC. Đồng hồ thứ nhất đặt trong không khí và cái thứ hai đặt trong chân không. Biết khối lượng riêng của không khí là = 1,3 kg/m3 . Biết các điều kiện khác giống hệt nhau khi hai đồng hồ hoạt động. Nếu xem đồng hồ thứ hai chạy đúng thì đồng hồ thứ nhất chạy nhanh hay chậm bao nhiêu sau một ngày đêm? A. chậm 6, 65 s B. chậm 0.665 s C. chậm 6,15 s D. chậm 6, 678 s
Theo dõi (0) 1 Trả lời -


Tính lực căng dây khi vật ở vị trí cao nhất của một con lắc đơn có dây treo dài l= 50cm gắn vật m=250g
bởi Phạm Khánh Ngọc
 14/09/2018
14/09/2018
Một con lắc đơn có dây treo dài \(l\)= 50cm gắn vật m=250\(g\). Truyền cho vật vận tốc \(v\)=1m/s theo phương ngang khi vật đang đứng yên tại vị trí cân bằng. Lấy \(g\)= 10m/\(s^2\) . Bỏ qua lực cản. Lực căng dây khi vật ở vị trí cao nhất là:
Theo dõi (0) 1 Trả lời -


Tính biên độ góc của 1 con lắc đơn sau khi qua VTCB vướng đinh nằm trên đường thẳng đứng cách điểm treo đoạn l/2
bởi Nguyễn Lê Thảo Trang
 14/09/2018
14/09/2018
Một CLD chiều dài l. Bên độ góc Ao=30°. Khi qua VTCB vướng đinh nằm trên đường thẳng đứng cách điểm treo đoạn l/2. Tính biên độ góc beta sau khi vướng đinh
Theo dõi (0) 1 Trả lời





