Giải bài 57 tr 89 sách GK Toán 9 Tập 2
Trong các hình sau, hình nào nội tiếp được một đường tròn: Hình bình hành, hình chữ nhật, hình vuông, hình thang, hình thang vuông, hình thang cân ? Vì sao?
Hướng dẫn giải chi tiết bài 57
Với bài 57 này, chúng ta sẽ sử dụng kiến thức đơn giản đó là nếu tứ giác có tổng hai số đo góc đối bằng 180 độ thì tứ giác đó nội tiếp.
Hình bình hành nói chung không nội tiếp được đường tròn vì tổng hai góc đối diện không bằng 180 độ, trường hợp cụ thể:
.png)
Hình chữ nhật hoàn toàn có thể nội tiếp được đường tròn, vì tổng hai góc đối bằng 180 độ.
.png)
Hình vuông là một trường hợp đặc biệt của hình chữ nhật, nên có thể nội tiếp đường tròn. Cụ thể:
.png)
Hình thang nói chung, hình thang vuông không nội tiếp được đường tròn, cụ thể đó là tổng hai góc đối chưa chắc bằng 180 độ. Trường hợp cụ thể:
.png)
Hình thang cân ABCD (BC= AD) có hai góc ở mỗi đáy bằng nhau thì hoàn toàn có thể nội tiếp đường tròn, cụ thể là:
.png)
Nhận xét rằng, hình thang nội tiếp đường tròn chắc chắn là hình thang cân!
-- Mod Toán 9 HỌC247
-


Cho tam giác ABC các góc nhọn, nội tiếp đường tròn (O). Hai đường cao BD và CE cắt nhau tại H
bởi Nguyễn Hoàng Phương Vy
 25/05/2020
25/05/2020
 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -

Cho đường tròn tâm O. trên đường tròn tâm O lấy điểm C( C không trùng với AB CA>CB. Các tiếp tuyến của đường tròn tâm O tại A, tại C cắt nhau ở điểm D, kẻ CH vuông góc với AB(H thuộc AB), DO cắt AC tại E. a) CM Tứ giác OECH nội tiếp b) Đg thẳng CD cắt đg thẳng AB tại F. Cm 2 gócBCF gócCFB=90 c)BD cắt CH tại M. Cm EM//AB
bởi Thu Trang
 22/05/2020
22/05/2020
a) CM Tứ giác OECH nội tiếp
b) Đg thẳng CD cắt đg thẳng AB tại F. Cm 2 gócBCF gócCFB=90
c)BD cắt CH tại M. Cm EM//AB
Theo dõi (0) 0 Trả lời -


Chứng minh AB.AM = AC.AN?
bởi Ngọc Diệu
 16/05/2020
16/05/2020
Giúp em giải bài này vs ạ
 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Chứng minh OF vuông góc với AB?
bởi Thanh Thương
 15/05/2020
15/05/2020
Câu 7
 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Chứng minh 3 điểm C; O;E thẳng hàng
bởi Ng Thị Thanh Trúc
 09/05/2020
a)Chứng minh 3 điểm C; O;E thẳng hàngb)tứ giác CDKI có nội tiếp đường tròn nào không? Vì sao?
09/05/2020
a)Chứng minh 3 điểm C; O;E thẳng hàngb)tứ giác CDKI có nội tiếp đường tròn nào không? Vì sao?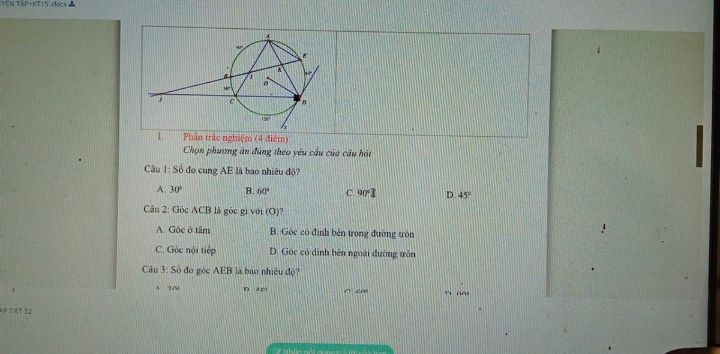 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -

 Toán 9
Toán 9 Theo dõi (1) 0 Trả lời
Theo dõi (1) 0 Trả lời -


Chứng minh BH vuông góc AC và tứ giác BEHD nội tiếp biết từ điểm M nằm ngoài đường tròn ( O, R ) vẽ tiếp tuyến MA và cát tuyến MBC
bởi Ngọc Châu
 07/05/2020
Từ điểm M nằm ngoài đường tròn ( O, R ) vẽ tiếp tuyến MA và cát tuyến MBC. Đường cao AD, CE trong tam giác ABC cắt nhau tại H. N là trung điểm của BC. a) Chứng minh BH vuông góc AC và tứ giác BEHD nội tiếp. b) Chứng minh MA2 = MB.MC c) Kéo dài AN cắt ( O ) tại F. So sánh NF và NH.Theo dõi (1) 0 Trả lời
07/05/2020
Từ điểm M nằm ngoài đường tròn ( O, R ) vẽ tiếp tuyến MA và cát tuyến MBC. Đường cao AD, CE trong tam giác ABC cắt nhau tại H. N là trung điểm của BC. a) Chứng minh BH vuông góc AC và tứ giác BEHD nội tiếp. b) Chứng minh MA2 = MB.MC c) Kéo dài AN cắt ( O ) tại F. So sánh NF và NH.Theo dõi (1) 0 Trả lời -


Chứng minh tứ giác OMED nội tiếp
bởi cao quoc hao
 29/04/2020
29/04/2020
 Theo dõi (1) 0 Trả lời
Theo dõi (1) 0 Trả lời -


Chứng minh tứ giác CKID nội tiếp?
bởi Ngọc Bảo
 24/04/2020
Nhờ các bạn giúp mình bài này kèm hình vẽ hộ ạ. Cảm ơn các bạn
24/04/2020
Nhờ các bạn giúp mình bài này kèm hình vẽ hộ ạ. Cảm ơn các bạn Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Chứng minh tứ giác ABDC nội tiếp?
bởi Thư Minh
 24/04/2020
24/04/2020
 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Chứng minh NC^2 = NE.NF?
bởi Hà Kiều
 23/04/2020
23/04/2020
 Theo dõi (1) 0 Trả lời
Theo dõi (1) 0 Trả lời
Bài tập SGK khác
Bài tập 55 trang 89 SGK Toán 9 Tập 2
Bài tập 56 trang 89 SGK Toán 9 Tập 2
Bài tập 58 trang 90 SGK Toán 9 Tập 2
Bài tập 59 trang 90 SGK Toán 9 Tập 2
Bài tập 60 trang 90 SGK Toán 9 Tập 2
Bài tập 39 trang 106 SBT Toán 9 Tập 2
Bài tập 40 trang 106 SBT Toán 9 Tập 2
Bài tập 41 trang 106 SBT Toán 9 Tập 2
Bài tập 42 trang 107 SBT Toán 9 Tập 2
Bài tập 43 trang 107 SBT Toán 9 Tập 2





