Giải bài 56 tr 89 sách GK Toán 9 Tập 2
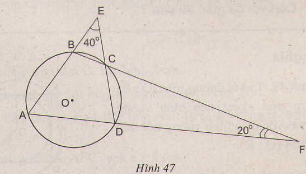
Xem hình 47. Hãy tìm số đo các góc của tứ giác ABCD
Hướng dẫn giải chi tiết bài 56
Với bài 56, ta sẽ vẽ lại hình, sử dụng tính chất các góc đã học và tứ giác nội tiếp để tính số đo các góc đề bài yêu cầu.
.png)
Ta có:
\(\small \widehat{BCE}=\widehat{DCF}\)
\(x=\widehat{BCE}=\widehat{DCF}(x>0^o)\)
Theo tính chất góc ngoài tam giác, ta có:
\(\widehat{ABC}=40^o+x\)
\(\widehat{ADC}=20^o+x\)
Mặc khác, tứ giác ABCD nội tiếp nên:
\(\widehat{ABC}+\widehat{ADC}=180^o\)
\(\Rightarrow 40^o+x+20^o+x=180^o\Rightarrow x=60^o\)
\(\Rightarrow \widehat{ABC}=60^o+40^o=100^o\)
\(\Rightarrow \widehat{ADC}=180^o-100^o=80^o\)
\(\Rightarrow \widehat{BCD}=180^o-x=120^o\)
\(\Rightarrow \widehat{BAD}=180^o-120^o=60^o\)
-- Mod Toán 9 HỌC247
-
Chứng minh các tứ giác AECD, BDCF nội tiếp?
bởi Thúy Ngọc Nguyễn
10/06/2020
Giải toán hình
Theo dõi (0) 0 Trả lời -
Chứng minh tứ giác ADHE nội tiếp đường tròn?
bởi Phương Phương
09/06/2020
Giúp mình đi!!! Mình cần liền
Cho tam giác ABC có 3 góc nhọn, đường tròn tâm O đường kính BC cât cạnh AB tại D và cắt cạnh AC tại E. Gọi H là giao điểm của BE và CD.
a) Chứng minh tứ giác ADHE nội tiếp đường tròn.
b) Gọi I là trung điểm của AH, chứng minh IO vuông góc với DE.
c) AD*AB=AE*AC
Theo dõi (0) 0 Trả lời -
Chứng minh ABED là tứ giác nội tiếp và \(\widehat {EBD} = \widehat {EFC}\)?
bởi Nguyễn Mỹ Tiên
09/06/2020
Cho tam giác abc vuông tại a, D là đường túy ý theo cạnh ac. DE vuông góc BC . CM ABED LÀ TỨ GIÁC NỘI TIÉP. F LÀ GIAO ĐIỂM CỦA BA và DE. Cm GÓC EBD=EFC
Theo dõi (0) 0 Trả lời -
Chứng minh AIMD là tứ giác nội tiếp?
bởi Nguyễn Yến Nhi
06/06/2020
Làm giúp mình câu 5b vs
Theo dõi (0) 0 Trả lời -
Chứng minh rằng tứ giác KIHB nội tiếp?
bởi Nhật Linh
05/06/2020
Vẽ hình giải câu b, c giúp mik
Theo dõi (0) 0 Trả lời -
Chứng minh tứ giác ABDC nội tiếp?
bởi Ly Hà
05/06/2020
.
Theo dõi (0) 0 Trả lời -
Chứng minh CKNH nội tiếp?
bởi Trần Hương
05/06/2020
Từ điểm M nằm ngoài đường tròn kẻ 2 tiếp tuyến MA, MB của đường tròn (O) . Tia Mx nằm giữa 2 tia MO và MA, tia Mx cắt (O) tại C và D( C nằm giữa M và D) và cắt AB tại N. Gọi K là trung điểm CD, H là giao điểm AB và MO. Chứng minh:
a) CKNH nội tiếp
b) MC.MD=MN.MK
c) Tam giác BCK đồng dạng với tam giác BAD
d) Có đường thẳng đi qua H vuông góc OA và cắt AC tại E, AD tại F. Chứng minh HE=HF
Theo dõi (0) 0 Trả lời -
Chứng minh tứ giác BCED nội tiếp ?
bởi Hoàng Thắm
04/06/2020
Theo dõi (0) 0 Trả lời -
Chứng minh M, H, K thẳng hàng?
bởi Bùi Duy
31/05/2020
.
Theo dõi (0) 0 Trả lời -
Chứng minh tứ giác AECF nội tiếp?
bởi Hiếu Vũ Đình
30/05/2020
Giải hộ mình vs ạ
Cho 2 đường tròn tâm O và tâm M cắt nhau tại A, B,. Gọi E, F là tiếp tuyến chung của 2 đường tròn, EF cắt AB ở I, C là điểm đối xứng với B qua I. Chứng minh tứ giác AECF nội tiếp
Theo dõi (0) 0 Trả lời -
Cho tam giác ABC các góc nhọn, nội tiếp đường tròn (O). Hai đường cao BD và CE cắt nhau tại H
bởi Nguyễn Hoàng Phương Vy
25/05/2020
Theo dõi (0) 0 Trả lời
Bài tập SGK khác
Bài tập 54 trang 89 SGK Toán 9 Tập 2
Bài tập 55 trang 89 SGK Toán 9 Tập 2
Bài tập 57 trang 89 SGK Toán 9 Tập 2
Bài tập 58 trang 90 SGK Toán 9 Tập 2
Bài tập 59 trang 90 SGK Toán 9 Tập 2
Bài tập 60 trang 90 SGK Toán 9 Tập 2
Bài tập 39 trang 106 SBT Toán 9 Tập 2
Bài tập 40 trang 106 SBT Toán 9 Tập 2
Bài tập 41 trang 106 SBT Toán 9 Tập 2
Bài tập 42 trang 107 SBT Toán 9 Tập 2
Bài tập 43 trang 107 SBT Toán 9 Tập 2
