Giải bài 66 tr 15 sách BT Toán lớp 9 Tập 1
Tìm x, biết:
a) \(\sqrt {{x^2} - 9} - 3\sqrt {x - 3} = 0\);
b) \(\sqrt {{x^2} - 4} - 2\sqrt {x + 2} = 0\).
Hướng dẫn giải chi tiết
Hướng dẫn giải
Áp dụng:
Để \(\sqrt A \) có nghĩa \(A \ge 0\)
Với \(A \ge 0;B \ge 0\)
\(\sqrt A = B \Leftrightarrow A = {B^2}.\)
\(\sqrt {A.B} = \sqrt A .\sqrt B. \)
Lời giải chi tiết
a) Điều kiện: \(x - 3 \ge 0 \Leftrightarrow x \ge 3\)
Ta có:
\(\eqalign{
& \sqrt {{x^2} - 9} - 3\sqrt {x - 3} = 0 \cr
& \Leftrightarrow \sqrt {(x + 3)(x - 3)} - 3\sqrt {x - 3} \cr} \)
\(\eqalign{
& \Leftrightarrow \sqrt {x - 3} (\sqrt {x + 3} - 3) = 0 \cr
& \Leftrightarrow \sqrt {x - 3} = 0 \cr} \) hoặc \(\sqrt {x + 3} - 3 = 0\)
+) \(\sqrt {x - 3} = 0 \Leftrightarrow x - 3 = 0 \Leftrightarrow x = 3\) (thỏa mãn)
+) \(\eqalign{
& \sqrt {x + 3} - 3 = 0 \Leftrightarrow \sqrt {x + 3} = 3 \cr
& \Leftrightarrow x + 3 = 9 \Leftrightarrow x = 6 \cr} \) (thỏa mãn)
Vậy x = 3 và x = 6.
b) Điều kiện: \(x \ge 2\) hoặc x = -2
Ta có:
\(\eqalign{
& \sqrt {{x^2} - 4} - 2\sqrt {x + 2} = 0 \cr
& \Leftrightarrow \sqrt {(x + 2)(x - 2)} - 2\sqrt {x + 2} = 0 \cr} \)
\(\eqalign{
& \Leftrightarrow \sqrt {x + 2} (\sqrt {x + 2} - 2) = 0 \cr
& \Leftrightarrow \sqrt {x + 2} = 0 \cr} $$ hoặc $$\sqrt {x - 2} - 2 = 0\)
+) \(\eqalign{
& \sqrt {x + 2} = 0 \Leftrightarrow x + 2 = 0 \cr
& \Leftrightarrow x = - 2 \cr} \) (thỏa mãn)
+) \(\eqalign{
& \sqrt {x - 2} - 2 = 0 \Leftrightarrow \sqrt {x - 2} = 2 \cr
& \Leftrightarrow x - 2 = 4 \Leftrightarrow x = 6 \cr} \) (thỏa mãn)
Vậy x = -2 và x = 6.
-- Mod Toán 9 HỌC247
-


Tính giá trị của biểu thức P=(√x+1)/(√x-2) khi x=36
bởi Nguyễn Hồng
 07/03/2020
Tính giá trị của biểu thức
07/03/2020
Tính giá trị của biểu thức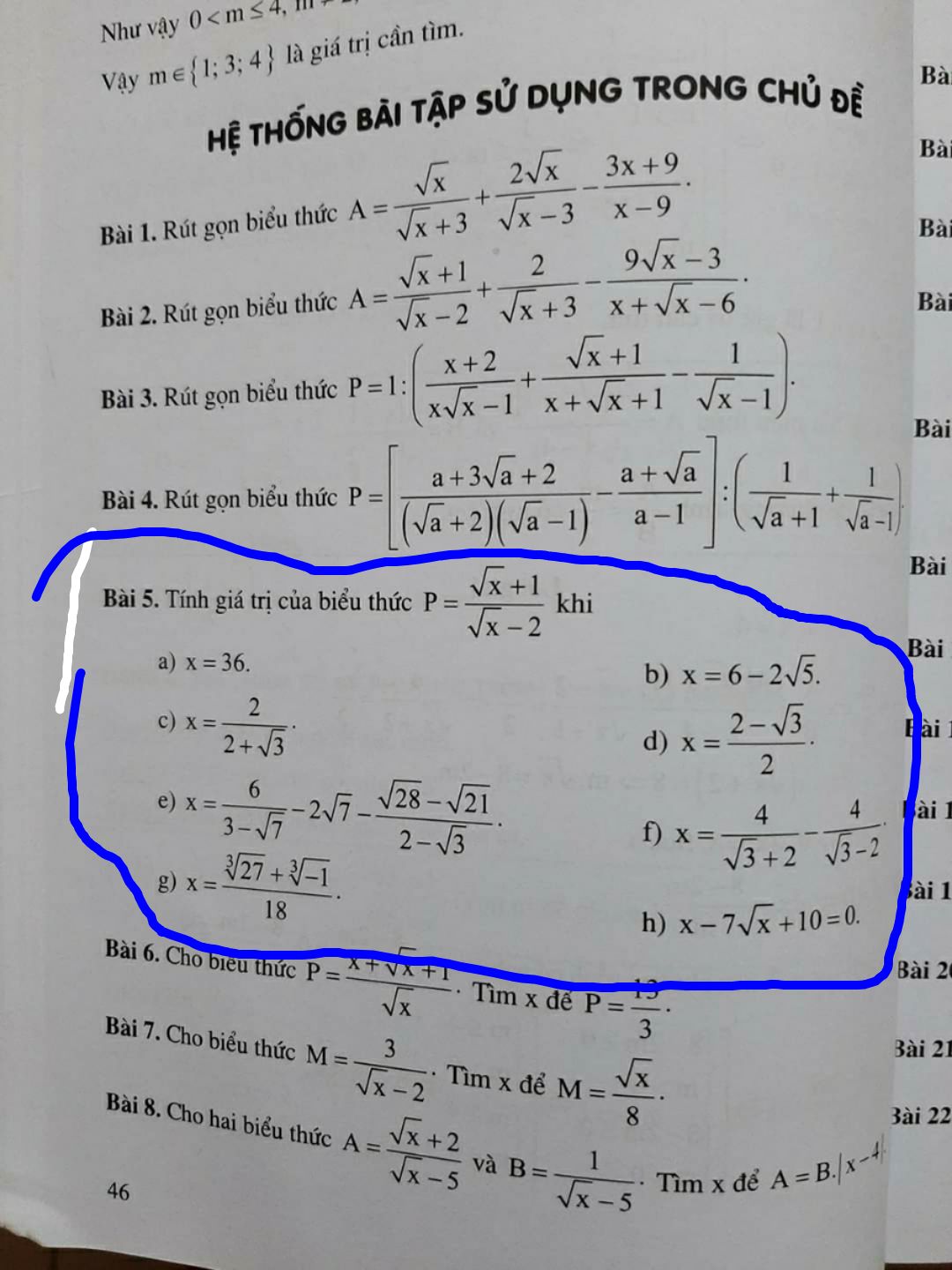 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Giải phương trình căn(4 - căn(4+x) = x
bởi Nguyễn Trung
 27/01/2020
27/01/2020
Giải phương trình:
Theo dõi (0) 3 Trả lời -


Chứng minh căn a^3 / a^3 + (b+c)^3 + căn b^3 / b^3 + (a+c)^3 + căn c^3/ ^3 + (a+b)^3 >=1
bởi Nhung Nhung
 19/01/2020
19/01/2020
Cho a,b,c dương. Chứng minh căn a^3 / a^3 + (b+c)^3 + căn b^3 / b^3 + (a+c)^3 + căn c^3/ ^3 + (a+b)^3 >=1
Theo dõi (0) 0 Trả lời -


Tìm GTLN của biểu thức
bởi Ngọc Nguyễn
 18/11/2019
Tìm GTLN của biểu thức sau
18/11/2019
Tìm GTLN của biểu thức sau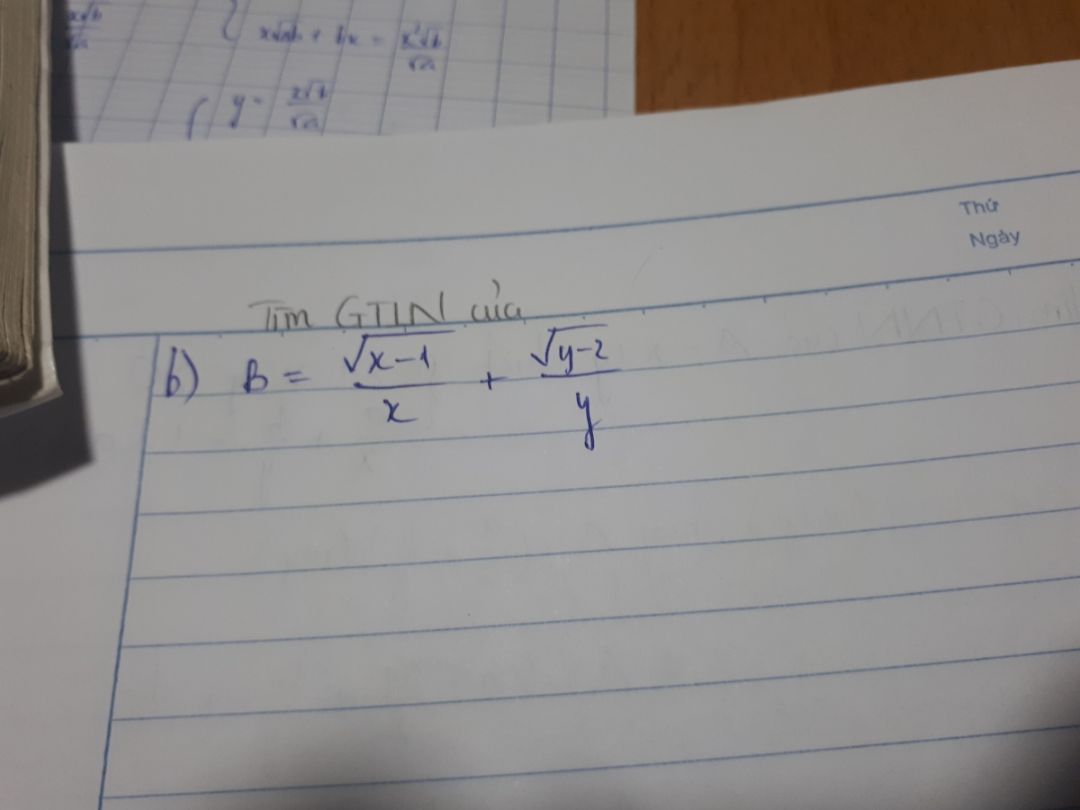 Theo dõi (1) 4 Trả lời
Theo dõi (1) 4 Trả lời -


Giải phương trình căn(x+1)+căn(4-x)+căn 4+3x-x^2=5
bởi mạnh lê
 01/09/2019
01/09/2019
gpt căn x+1 +căn 4-x +căn 4+3x-x^2 =5
mn
ơ i giúp e mai e đi hok rooifto be continued
Theo dõi (1) 14 Trả lời -


Giải phương trình x^2+căn(x^2+2019)=2019
bởi Tịch Hy
 23/08/2019
23/08/2019
Giải phương trình
x2 + √(x2 + 2019) = 2019.
x2 + 4x + 5 = 2√(2x+3)
Giúp em với ạ.
Theo dõi (0) 8 Trả lời -


Giải pt nghiệm nguyên xy+1=z (x,y,z nguyên tố)
bởi Linh Trần
 09/07/2019
09/07/2019
Giải ptnn
xy+1=z (x,y,z nguyên tố)
Theo dõi (0) 3 Trả lời -


Rút gọn biểu thức sau:
Theo dõi (0) 3 Trả lời -


Phân tích thành nhân tử x-6 căn x+9 với x > = 0
bởi Nguyễn Thu
 18/06/2019
18/06/2019
phân tích thành nhân tử
a, x - 1 (x >= 0)
b, x - 5 (x >= 0)
c, x - 6√x+ 9 ( x >= 0)
d, x - 4√x+ 4 ( x >= 0)
Theo dõi (1) 9 Trả lời -


Chứng minh nếu P=0 thì (x^1999+y^1999) (y^2001+z^2001) (z^2015+x^2015)=0
bởi Phan Bao Ngoc
 14/06/2019
14/06/2019
Cho đa thức P = (x+y+z)^3 - x^3 - y^3 - z^3. Chứng tỏ :
a) Nếu P = 0 thì (x^1999 + y^1999) (y^2001 + z^2001) (z^2015 + x^2015) = 0
b) Nếu x, y, z là các số nguyên cùng chẵn lẽ thì P chia hết cho 24
Theo dõi (1) 2 Trả lời -


Tìm x biết (x^2+x+2)^3-(x+1)^3=x^6+1
bởi Phan Bao Ngoc
 14/06/2019
14/06/2019
Tìm x biết : (x^2+x+2)^3-(x+1)^3=x^6+1
Giúp mình vs nhaaa
 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời
Bài tập SGK khác
Bài tập 64 trang 15 SBT Toán 9 Tập 1
Bài tập 65 trang 15 SBT Toán 9 Tập 1
Bài tập 67 trang 15 SBT Toán 9 Tập 1
Bài tập 6.1 trang 16 SBT Toán 9 Tập 1
Bài tập 68 trang 16 SBT Toán 9 Tập 1
Bài tập 69 trang 16 SBT Toán 9 Tập 1
Bài tập 70 trang 16 SBT Toán 9 Tập 1
Bài tập 71 trang 16 SBT Toán 9 Tập 1
Bài tập 72 trang 17 SBT Toán 9 Tập 1
Bài tập 73 trang 17 SBT Toán 9 Tập 1
Bài tập 74 trang 17 SBT Toán 9 Tập 1
Bài tập 75 trang 17 SBT Toán 9 Tập 1
Bài tập 76 trang 17 SBT Toán 9 Tập 1
Bài tập 77 trang 17 SBT Toán 9 Tập 1
Bài tập 78 trang 17 SBT Toán 9 Tập 1
Bài tập 79 trang 17 SBT Toán 9 Tập 1






