Bài tập 43 trang 128 SGK Toán 9 Tập 1

Hướng dẫn giải

a) Áp dụng định lí về đường kính vuông góc với dây thì đi qua trung điểm dây đó và định lí về đường trung bình của hình thang.

b) Áp dụng tính chất hai đường tròn cắt nhau và tính chất đường trung bình trong tam giác để chứng minh.

Lời giải chi tiết

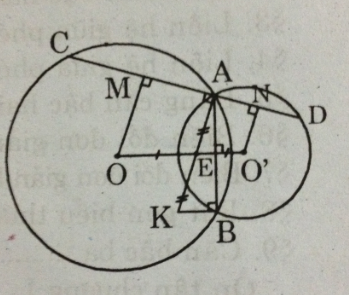
a) Vẽ OM ⊥ AC tại M, O’N ⊥AD tại N. 

Xét đường tròn (O), vì \(\displaystyle OM \bot AC \Rightarrow MA = MC = {{AC} \over 2}\) (định lý đường kính vuông góc với dây)

Xét đường tròn (O'), vì \(\displaystyle O’N ⊥AD \Rightarrow NA = N{\rm{D}} = {{A{\rm{D}}} \over 2}\) (định lý đường kính vuông góc với dây)

Mặt khác, ta có \(OM ⊥ CD, IA ⊥ CD, O’N ⊥ CD\)  

\(⇒ OM // IA //O’N.\) 

Suy ra tứ giác OMNO' là hình thang.

Hình thang OMNO’ có \(IA // OM//O'N; IO = IO’\) nên \(MA  = NA\) (đường thẳng song song với hai đáy của hình thang và đi qua trung điểm 1 cạnh bên thì đi qua trung điểm cạnh bên còn lại)

Do vậy \(2.MA=2.NA\) hay \(AC = AD.\) 

b) Ta có (O) và (O’) cắt nhau tại A, B 

⇒ OO’ là đường trung trực của đoạn thẳng AB (tính chất đường nối tâm của hai đường tròn cắt nhau)

\(⇒ IA = IB\) (tính chất đường trung trực của đoạn thẳng)

Mặt khác \(IA = IK\) ( vì K đối xứng với A qua I)

Do đó: \(IA = IB = IK\)

Ta có ∆KBA có BI là đường trung tuyến và \(\displaystyle BI = {{AK} \over 2}\) nên ∆KBA vuông tại B

\(⇒ KB ⊥ AB\) 

-- Mod Toán 9 HỌC247