Giải bài 8 tr 63 sách GK Toán 8 Tập 2
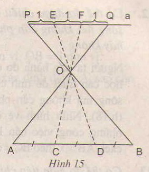
a) Để chi đoạn thẳng AB thành ba đoạn bằng nhau, người ta đã làm như hình 15. Hãy mô tả cách làm trên và giải thích vì sao các đoạn AC,CD,DB bằng nhau?
b) Bằng cách tương tự, hãy chi đoạn thẳng AB cho trước thành 5 đoạn bằng nhau. Hỏi có cách nào khác với cách làm trên mà vẫn có thể chia đoạn AB cho trước thành 5 đoạn bằng nhau?
Hướng dẫn giải chi tiết
Câu a:
Hãy mô tả cách làm trên và giải thích vì sao các đoạn AC, CD, DB bằng nhau?
Mô tả cách làm:
Vẽ đoạn \(PQ\) song song với \(AB, PQ\) có độ dài bằng \(3\) đơn vị
- Trên PQ lấy lần lượt các điểm E, F sao cho \(PE=EF=FQ=1\) đơn vị
- Xác định giao điểm \(O\) của hai đoạn thẳng \(PB\) và \(QA\).
- Vẽ các đường thẳng \(EO, FO\) cắt \(AB\) tại \(C\) và \(D\).
Chứng minh \(AC= CD = DB\)
\(∆OPE\) và \(∆OBD\) có \(PE//DB\) (theo cách vẽ) nên \(\dfrac{DB}{PE} = \dfrac{OD}{OE}\) (1) (hệ quả định lý TaLet)
\(∆OEF\) và \(∆ODC\) có \(EF // CD\) (theo cách vẽ) nên \(\dfrac{CD}{EF} = \dfrac{OD}{OE}=\dfrac{OC}{OF}\) (2) (hệ quả định lý TaLet)
\(∆OFQ\) và \(∆OCA\) có \(FQ // AC\) (theo cách vẽ) nên \(\dfrac{AC}{FQ} = \dfrac{OC}{OF}\) (3) (hệ quả định lý TaLet)
Từ (1), (2) và (3) suy ra:
\(\dfrac{DB}{PE} = \dfrac{CD}{EF}=\dfrac{AC}{FQ}\) mà \(PE = EF=FQ\) (gt) nên \(DB = CD=AC\).
Vây: \(DB = CD = AC\).
Câu b:
Tương tự chia đoạn thẳng AB thành 5 đoạn bằng nhau thực hiện như hình vẽ sau:
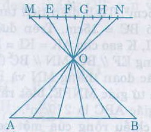
Ta có thể chia đoạn thẳng AB thành 5 đoạn thẳng bằng nhau như cách sau:
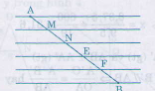
Vẽ 6 đường thẳng song song cách đều nhau( có thể dùng thước kẻ để vẽ liên tiếp). Đặt đầu mút A và B ở hai đường thẳng ngoài cùng thì các đường thẳng song song căt AB chia thành 5 phần bằng nhau.
-- Mod Toán 8 HỌC247
-


Một tấm bảng hình vuông có cạnh 20cm để trước máy chiếu và thấy được bóng trên tường có diện tích 4m2. Hỏi máy chiếu để cách bức tường bao xa? Biết rằng tấm bảng để cách máy chiếu 30cm
bởi Trịnh Lan Trinh
 30/05/2020
Theo dõi (0) 1 Trả lời
30/05/2020
Theo dõi (0) 1 Trả lời -


Một chiếc máy chiếu để cách màn chiếu 3m. Bạn An vô tình để tấm bảng hình vuông trước máy chiếu và cách máy chiếu 30cm thì thấy được bóng tấm bảng trên màn chiếu có diện tích 4m2. Hỏi kích thước tấm bảng ?
bởi Trần Hoàng Mai
 31/05/2020
Theo dõi (0) 1 Trả lời
31/05/2020
Theo dõi (0) 1 Trả lời -


Tính độ dài cạnh BC, DC?
bởi Nguyễn Lê Trúc Quỳnh
 25/05/2020
25/05/2020
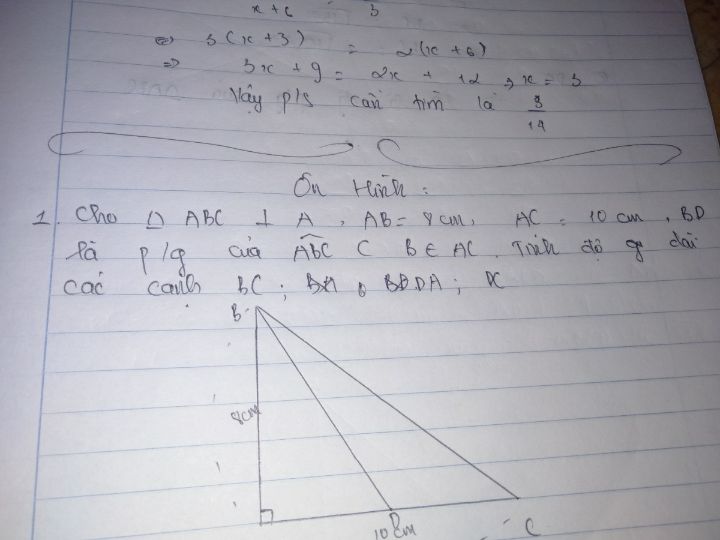 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời
Bài tập SGK khác
Bài tập 6 trang 62 SGK Toán 8 Tập 2
Bài tập 7 trang 62 SGK Toán 8 Tập 2
Bài tập 9 trang 63 SGK Toán 8 Tập 2
Bài tập 10 trang 63 SGK Toán 8 Tập 2
Bài tập 11 trang 63 SGK Toán 8 Tập 2
Bài tập 12 trang 64 SGK Toán 8 Tập 2
Bài tập 13 trang 64 SGK Toán 8 Tập 2
Bài tập 14 trang 64 SGK Toán 8 Tập 2
Bài tập 6 trang 84 SBT Toán 8 Tập 2
Bài tập 7 trang 84 SBT Toán 8 Tập 2
Bài tập 8 trang 84 SBT Toán 8 Tập 2
Bài tập 9 trang 84 SBT Toán 8 Tập 2
Bài tập 10 trang 84 SBT Toán 8 Tập 2
Bài tập 11 trang 85 SBT Toán 8 Tập 2
Bài tập 12 trang 85 SBT Toán 8 Tập 2
Bài tập 13 trang 85 SBT Toán 8 Tập 2
Bài tập 14 trang 85 SBT Toán 8 Tập 2
Bài tập 15 trang 86 SBT Toán 8 Tập 2
Bài tập 16 trang 86 SBT Toán 8 Tập 2
Bài tập 2.1 trang 86 SBT Toán 8 Tập 2





