Giải bài 10 tr 63 sách GK Toán 8 Tập 2
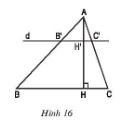
Tam giác ABC có đường cao AH. Đường thẳng d song song với BC, cắt các cạnh AB,AC và đường cao AH theo thứ tự tại các điểm B', C' và H'(h.16)
a) Chứng minh rằng: \(\frac{{AH'}}{{AH}} = \frac{{B'C'}}{{BC}}\)
b) Áp dụng: Cho biết \(AH' = \frac{1}{3} AH\) và diện tích tam giác ABC là 67.5 cm2. Tính diện tích tam giác AB'C'.
Hướng dẫn giải chi tiết
Câu a:
Chứng minh \(\frac{{AH'}}{{AH}} = \frac{{B'C'}}{{BC}}\)
Vì B'C' // với BC ⇒\(\frac{{B'C'}}{{BC}} = \frac{{AB'}}{{AB}}\) (1)
Trong ∆ABH có BH' // BH ⇒\(\frac{{AH'}}{{AH}} = \frac{{AB'}}{{BC}}\) (2)
Từ 1 và 2 ⇒\(\frac{{B'C'}}{{BC}} = \frac{{AH'}}{{AH}}\)
Câu b:
B'C' // BC mà AH ⊥ BC nên AH' ⊥ B'C' hay AH' là đường cao của tam giác AB'C'.
Áp dụng kết quả câu a) ta có: AH' = \(\frac{1}{3}\) AH
\(\frac{{B'C'}}{{BC}} = \frac{{AH'}}{{AH}}\) = \(\frac{1}{3}\) ⇒ B'C' = \(\frac{1}{3}\) BC
⇒ SAB’C’= \(\frac{1}{2}\) AH'.B'C' = \(\frac{1}{2}\).\(\frac{1}{3}\)AH.\(\frac{1}{3}\)BC
⇒ SAB’C’= (\(\frac{1}{2}\)AH.BC)\(\frac{1}{9}\)
mà SABC= \(\frac{1}{2}\)AH.BC = 67,5 cm2
Vậy SAB’C’= \(\frac{1}{9}\).67,5= 7,5 cm2
-- Mod Toán 8 HỌC247
-

 Cho tam giác ABC cân tại B, BA=BC=a, AC=b. Đường phân giác góc A cắt BC tại M, đường phân giác góc C cắt BA tại N. A) Chứng minh MN//AC. B) Tính MN theo a và b.Theo dõi (0) 0 Trả lời
Cho tam giác ABC cân tại B, BA=BC=a, AC=b. Đường phân giác góc A cắt BC tại M, đường phân giác góc C cắt BA tại N. A) Chứng minh MN//AC. B) Tính MN theo a và b.Theo dõi (0) 0 Trả lời -


Chứng minh EF//CD?
bởi Tú Tây
 23/04/2020
cần gấp
23/04/2020
cần gấp Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Tính độ dài các đoạn thẳng NC và BC biết tam giác ABC vuông tại A, điểm M thuộc cạnh AB
bởi Nhi Dương Thị Liên
 22/04/2020
Tam giác ABC vuông tại A, điểm M thuộc cạnh AB, điểm N thuộc AC sao cho AM =6cm, AN =12cm ,AB=24,MN/BC . Tính độ dài các đoạn thẳng NC và BCTheo dõi (1) 2 Trả lời
22/04/2020
Tam giác ABC vuông tại A, điểm M thuộc cạnh AB, điểm N thuộc AC sao cho AM =6cm, AN =12cm ,AB=24,MN/BC . Tính độ dài các đoạn thẳng NC và BCTheo dõi (1) 2 Trả lời
Bài tập SGK khác
Bài tập 8 trang 63 SGK Toán 8 Tập 2
Bài tập 9 trang 63 SGK Toán 8 Tập 2
Bài tập 11 trang 63 SGK Toán 8 Tập 2
Bài tập 12 trang 64 SGK Toán 8 Tập 2
Bài tập 13 trang 64 SGK Toán 8 Tập 2
Bài tập 14 trang 64 SGK Toán 8 Tập 2
Bài tập 6 trang 84 SBT Toán 8 Tập 2
Bài tập 7 trang 84 SBT Toán 8 Tập 2
Bài tập 8 trang 84 SBT Toán 8 Tập 2
Bài tập 9 trang 84 SBT Toán 8 Tập 2
Bài tập 10 trang 84 SBT Toán 8 Tập 2
Bài tập 11 trang 85 SBT Toán 8 Tập 2
Bài tập 12 trang 85 SBT Toán 8 Tập 2
Bài tập 13 trang 85 SBT Toán 8 Tập 2
Bài tập 14 trang 85 SBT Toán 8 Tập 2
Bài tập 15 trang 86 SBT Toán 8 Tập 2
Bài tập 16 trang 86 SBT Toán 8 Tập 2
Bài tập 2.1 trang 86 SBT Toán 8 Tập 2