Giải bài 12 tr 64 sách GK Toán 8 Tập 2
Có thể đo dược chiều rông của một khúc sông mà không cần phải sang bờ bên kia hay không?
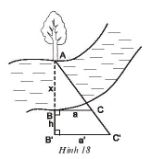
Người ta tiền hành đo đạc các yếu tố hình học cần thiết để tình chiều rộng của khúc sông mà không cần phải sang bờ bên kia(h18). Nhìn hình vẽ, Hãy mô tả những công việc cần làm và tính khoảng cách AB=x theo BC=a a, B'C'= a', BB'= h.
Hướng dẫn giải chi tiết
Mô tả cách làm:
* Chọn một điểm A cố định bên mép bờ sông bên kia (chẳng hạn như là một thân cây), đặt hai điểm B và B' thẳng hàng với A, điểm B sát mép bờ còn lại và \(AB\) chính là khoảng cách cần đo.
* Trên hai đường thẳng vuông góc với \(AB'\) tại \(B\) và \(B'\) lấy \(C\) và \(C'\) sao cho \(A,C,C'\) thẳng hàng.
* Đo độ dài các đoạn \(BB'= h, BC= a, B'C'= a'\). Từ đó ta sẽ tính được đoạn \(AB=x.\)
Ta có: \(BC ⊥ AB’\) và \(B’C’ ⊥ AB’ ⇒ BC // B’C’\)
Xét \(ΔAB’C’\) có \(BC // B’C’ \,(B ∈ AB’, C ∈ AC’) \)
\(⇒ \dfrac{AB}{AB'} = \dfrac{BC}{BC'}\) (hệ quả định lý Talet) mà \(AB' = x + h\) nên
\(\dfrac{x}{x+ h} = \dfrac{a}{a'}\)
\( \Leftrightarrow a'x = ax + ah\)
\( \Leftrightarrow a'x - ax = ah\)
\(\Leftrightarrow x(a' - a) = ah\)
\( \Rightarrow x= \dfrac{ah}{a'-a}\)
Vậy khoảng cách \(AB\) bằng \(\dfrac{ah}{a'-a}\)
-- Mod Toán 8 HỌC247
-


Chứng minh IE = IF?
bởi Thảo Phương Nguyễn
 11/04/2020
11/04/2020
 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Chứng minh IE = IF?
bởi Thảo Phương Nguyễn
 09/04/2020
09/04/2020
Bài 2. Cho hình thang ABCD (AB//CD), AB = a, CD = b. Hai đường chéo cắt nhau tại I. Qua I kẻ đường thẳng song song với AB cắt AD tại E, cắt BC tại F.
a) Chứng minh IE = IF.
b) Tính EF theo a và b.
Theo dõi (0) 2 Trả lời -


Cho tam giác ABC, D là trung điểm BC, M là điểm trên AD, BM cắt AC tại P, CM cắt AB tại Q. Chứng minh PQ//BC.
bởi Anh Duc
 31/03/2020
31/03/2020
 Theo dõi (0) 3 Trả lời
Theo dõi (0) 3 Trả lời
Bài tập SGK khác
Bài tập 10 trang 63 SGK Toán 8 Tập 2
Bài tập 11 trang 63 SGK Toán 8 Tập 2
Bài tập 13 trang 64 SGK Toán 8 Tập 2
Bài tập 14 trang 64 SGK Toán 8 Tập 2
Bài tập 6 trang 84 SBT Toán 8 Tập 2
Bài tập 7 trang 84 SBT Toán 8 Tập 2
Bài tập 8 trang 84 SBT Toán 8 Tập 2
Bài tập 9 trang 84 SBT Toán 8 Tập 2
Bài tập 10 trang 84 SBT Toán 8 Tập 2
Bài tập 11 trang 85 SBT Toán 8 Tập 2
Bài tập 12 trang 85 SBT Toán 8 Tập 2
Bài tập 13 trang 85 SBT Toán 8 Tập 2
Bài tập 14 trang 85 SBT Toán 8 Tập 2
Bài tập 15 trang 86 SBT Toán 8 Tập 2
Bài tập 16 trang 86 SBT Toán 8 Tập 2
Bài tập 2.1 trang 86 SBT Toán 8 Tập 2