Bài tập 12 trang 85 SBT Toán 8 Tập 2
Hình thang cân ABCD (AB // CD) có hai đường chéo AC và BD cắt nhau tại O (h.11). Gọi M, N theo thứ tự là trung điểm của BD và AC. Cho biết MD = 3MO, đáy lớn CD = 5,6cm.
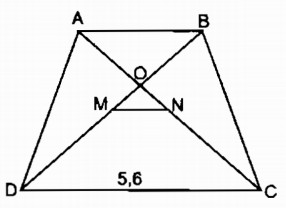
a. Tính độ dài đoạn thẳng MN và đáy nhỏ AB.
b. So sánh độ dài đoạn thẳng MN với nửa hiệu các độ dài của CD và AB.
Hướng dẫn giải chi tiết
- Hệ quả định lí Ta-lét: Nếu một đường thẳng cắt hai cạnh còn lại của một của một tam giác và song song với các cạnh còn lại thì nó tạo thành một tam giác mới có ba cạnh tương ứng tỉ lệ với ba cạnh còn lại của tam giác đã cho.
Hướng dẫn giải
- Định lí đảo của định lí Ta-lét: Nếu một đường thẳng cắt hai cạnh một tam giác và định ra trên hai cạnh ấy những đoạn thẳng tương ứng tỉ lệ thì đường thẳng đó song song với cạnh còn lại của tam giác.
Lời giải chi tiết
a) Vì \(ABCD\) là hình thang cân có \(AB // CD \) nên \(AD=BC\); \(AC = BD\)
Xét \(∆ADC\) và \(∆BCD\) có:
\(AC = BD\) (chứng minh trên)
\(AD = BC\) (chứng minh trên)
\(CD\) cạnh chung
\( \Rightarrow ∆ADC = ∆BCD\) (c.c.c)
\( \Rightarrow \widehat {ACD} = \widehat {BDC}\) (hai góc tương ứng)
Hay \(\widehat {OCD} = \widehat {ODC}\)
Do đó \(\Delta OCD\) cân tại \(O\).
\( \Rightarrow OC = OD \) (tính chất tam giác cân)
Ta có: \(AC=OA+OC\)
\(BD=OB+OD\)
Mà \(AC=BD;OC=OD\) nên \(OA = OB\)
Do đó \(MD=NC= \dfrac{1}{2}AC = \dfrac{1}{2}BD\)
\(OD=MO+MD\)
\(OC=NO+NC\)
Mà \(OD=OC;MD=NC\) nên \(MO=NO\)
Lại có: \(MD = 3MO\) (gt) \(⇒ NC = 3NO\)
Xét \(\Delta OCD\) có \(\displaystyle {{MO} \over {MD}} = {{NO} \over {NC}} = {1 \over 3}\)
Theo định lí đảo của định lí Ta-lét ta có \(MN // CD\).
Ta có: \(OD = OM + MD = OM + 3OM \)\(\,= 4OM\)
\(\Delta OCD\) có \(MN // CD\)
Theo hệ quả định lí Ta-lét ta có:
\(\displaystyle {{OM} \over {OD}} = {{MN} \over {CD}}\)
\(\displaystyle \Rightarrow {{MN} \over {CD}} = {{OM} \over {4OM}} = {1 \over 4}\)
\(\displaystyle \Rightarrow MN = {1 \over 4}CD = {1 \over 4}.5,6 = 1,4\) (cm)
Ta có: \(MB = MD\) (vì \(M\) là trung điểm \(BD\))
Suy ra: \(MB = 3OM\) hay \(OB = 2OM\)
\( AB // CD\) (gt), \(MN // CD\) (cmt) suy ra \(MN // AB\).
Xét \(\Delta OAB\) có \(MN // AB\)
Theo hệ quả định lí Ta-lét ta có:
\(\displaystyle{{OM} \over {OB}} = {{MN} \over {AB}}\)
\( \Rightarrow \displaystyle{{MN} \over {AB}} = {{OM} \over {2OM}} = {1 \over 2}\)
\( \Rightarrow AB = 2MN = 2.1,4 = 2,8\) (cm)
b) Ta có: \(\displaystyle{{CD - AB} \over 2} = {{5,6 - 2,8} \over 2} = {{2,8} \over 2}\)\(\, = 1,4\) (cm)
Vậy \(\displaystyle MN = {{CD - AB} \over 2}\).
-- Mod Toán 8 HỌC247
-


Chứng minh định lý Ta-lét đảo
bởi Nguyễn Thanh Hà
 31/05/2019
31/05/2019
Chứng minh định lý Ta-lét đảo ?
Theo dõi (0) 1 Trả lời -


Tìm giá trị x trong hình
bởi Lê Tường Vy
 31/05/2019
31/05/2019
tìm x trong hình sau
Theo dõi (0) 1 Trả lời -


Chứng minh AM vuông góc BC biết tam giác ABC có AB=AC, MK và MI vuông góc AB, AC
bởi A La
 09/04/2019
09/04/2019
Cho tam giác ABC có AB=AC. M là trung điểm của BC. Từ M kẻ MK và MI lần lượt vuông góc với AB, AC ( K thuộc AB, I thuoccj AC ). CMR:
a) AM vuông góc với BC
b) MK=MI và IK song song BC.
c) AM vuông góc IK.
GIúp mk vs! mk tik xho
Theo dõi (0) 1 Trả lời





