Giải bài 9 tr 84 sách BT Toán lớp 8 Tập 2
Hình thang ABCD (AB // CD) có hai đường chéo AC và BD cắt nhau tại O (h.8).
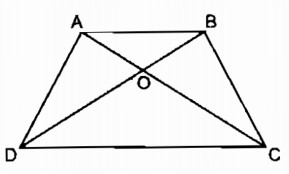
Chứng minh rằng: OA.OD = OB.OC.
Hướng dẫn giải chi tiết
Hướng dẫn giải
Sử dụng:
Hệ quả định lí Ta-lét: Nếu một đường thẳng cắt hai cạnh còn lại của một của một tam giác và song song với các cạnh còn lại thì nó tạo thành một tam giác mới có ba cạnh tương ứng tỉ lệ với ba cạnh còn lại của tam giác đã cho.
Lời giải chi tiết
Xét \(∆ OCD\) có \(AB // CD\) (gt)
Theo hệ quả định lí Ta-lét ta có:
\(\displaystyle{{OA} \over {OC}} = {{OB} \over {OD}}\)
\( \Rightarrow OA.OD = OB.OC\) (đpcm).
-- Mod Toán 8 HỌC247
-


Chứng minh H là trung điểm của BC biết tam giác ABC cân tại A có AB=13 cm
bởi Nguyễn Thị Thanh
 26/02/2019
26/02/2019
tam giác ABC cân tại A có AB= 13cm ; BC = 10 cm . AH vuông góc với BC
a, Chứng minh : H là trung điểm của BC
b, tính AH
c, Kẻ HE vuông góc với AB ; HF vuông góc với AC . chứng minh HE = HF
d, chứng minh EF // BC
Theo dõi (0) 1 Trả lời -


Tính FC biết AE =4cm,ED=2cm,BF=6cm
bởi Truc Ly
 31/05/2019
31/05/2019
Cho hình thang ABCD (AB//CD) . Kẻ 1 đường thẳng song song với 2 đáy cắt AD,BC tại E,F . Tính FC biết AE =4cm,ED=2cm,BF=6cm
Help meee ☹
Theo dõi (0) 1 Trả lời -


So sánh DE với BC biết AD =1/3 AB, đường thẳng qua D song song BC cắt AC tại E
bởi Nguyễn Bảo Trâm
 28/02/2019
28/02/2019
Cho tam giác ABC ; trên cạnh AB lấy điểm D sao cho AD =1/3 AB . Qua D kẻ đường thẳng song song với BC cắt AC tại E . So sánh DE với BC
Theo dõi (0) 1 Trả lời
Bài tập SGK khác
Bài tập 7 trang 84 SBT Toán 8 Tập 2
Bài tập 8 trang 84 SBT Toán 8 Tập 2
Bài tập 10 trang 84 SBT Toán 8 Tập 2
Bài tập 11 trang 85 SBT Toán 8 Tập 2
Bài tập 12 trang 85 SBT Toán 8 Tập 2
Bài tập 13 trang 85 SBT Toán 8 Tập 2
Bài tập 14 trang 85 SBT Toán 8 Tập 2
Bài tập 15 trang 86 SBT Toán 8 Tập 2
Bài tập 16 trang 86 SBT Toán 8 Tập 2
Bài tập 2.1 trang 86 SBT Toán 8 Tập 2





