Bài tập 11 trang 85 SBT Toán 8 Tập 2
Cho hình thang ABCD (AB // CD). Trên cạnh bên AD lấy điểm E sao cho \({{AE} \over {ED}} = {p \over q}\) . Qua E kẻ đường thẳng song song với các đáy và cắt BC tại F
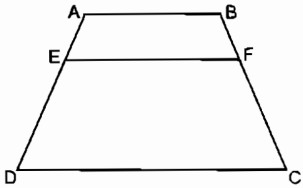
Chứng minh rằng: \(EF = {{p.CD + q.AB} \over {p + q}}\)
HD: Kẻ thêm đường chéo AC, cắt EF ở I, rồi áp dụng hệ quả định lí Ta-lét vào các tam giác ADC và CAB.
Hướng dẫn giải chi tiết
Hướng dẫn giải
- Định lí Ta-lét: Nếu một đường thẳng song song với một cạnh của tam giác và cắt hai cạnh còn lại thì nó định ra trên hai cạnh ấy những đoạn thẳng tương ứng tỉ lệ.
- Hệ quả định lí Ta-lét: Nếu một đường thẳng cắt hai cạnh còn lại của một của một tam giác và song song với các cạnh còn lại thì nó tạo thành một tam giác mới có ba cạnh tương ứng tỉ lệ với ba cạnh còn lại của tam giác đã cho.
- Tính chất tỉ lệ thức: \(\dfrac{a}{b} = \dfrac{c}{d} \Rightarrow \dfrac{a}{{a + b}} = \dfrac{c}{{c + d}}\)
Lời giải chi tiết
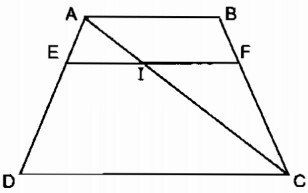
Kẻ đường chéo \(AC\) cắt \(EF\) tại \(I.\)
Áp dụng hệ quả định lí Ta-lét vào \(\Delta ADC \) có \(EI // CD\), ta có:
\(\displaystyle {{AE} \over {AD}} = {{EI} \over {CD}}\)
\( \Rightarrow \displaystyle EI = {{AE} \over {AD}}.CD\) (1)
Lại có: \(\displaystyle {{AE} \over {ED}} = {p \over q}\) (gt)
Áp dụng tính chất của tỉ lệ thức ta có:
\(\displaystyle {{AE} \over {ED}} = {p \over q}\)
\( \displaystyle\Rightarrow {{AE} \over {AE + ED}} = {p \over {p + q}}\)
Hay \( \displaystyle{{AE} \over {AD}} = {p \over {p + q}}\) (2)
Từ (1) và (2) suy ra: \(\displaystyle EI = {p \over {p + q}}.CD\)
Áp dụng định lí Ta-lét vào \(\Delta ABC\) có \(IF // AB\), ta có:
\(\displaystyle {{BF} \over {FC}} = {{AI} \over {IC}}\) (3)
Áp dụng định lí Ta-lét vào \(\Delta ADC\) có \(EI // CD\), ta có:
\(\displaystyle {{AE} \over {ED}} = {{AI} \over {IC}}\) (4)
Từ (3) và (4) suy ra: \(\displaystyle {{BF} \over {FC}} = {{AE} \over {ED}} = {p \over q}\)
Áp dụng hệ quả định lí Ta-lét vào \(\Delta ABC\) có \(IF // AB\), ta có:
\(\displaystyle {{IF} \over {AB}} = {{CF} \over {CB}}\)
\(\displaystyle \Rightarrow IF = {{CF} \over {CB}}.AB\) (5)
Ta có: \(\displaystyle {{BF} \over {CF}} = {p \over q}\) (cmt)
\(\displaystyle \Rightarrow {{CF} \over {BF}} = {q \over p}\)
Áp dụng tính chất của tỉ lệ thức ta có:
\(\displaystyle {{CF} \over {BF}} = {q \over p}\)
\(\displaystyle \Rightarrow {{CF} \over {CF + BF}} = {q \over {p + q}} \)
\(\displaystyle \Rightarrow {{CF} \over {CB}} = {q \over {p + q}}\) (6)
Từ (5) và (6) suy ra: \(\displaystyle IF = {q \over {p + q}}.AB\)
Vậy \(\displaystyle EF = EI + {\rm I}F \)\(\,\displaystyle = {p \over {p + q}}.CD + {q \over {p + q}}.AB \)\(\,\displaystyle = {{p.CD + q.AB} \over {p + q}}\)
-- Mod Toán 8 HỌC247
-


Chứng minh LF//AB và LF đi qua trung điểm BC
bởi My Hien
 31/05/2019
31/05/2019
cho tam giác ABC. kẻ phân giác trong BD, CK. từ A kẻ đường thẳng vuông góc với CK tại M, từ A, C kẻ các đường thẳng vuông góc với BD tại N và L tương ứng, MN cắt AC tại E, BF cắt CL tại E
a, chứng minh MN//BC
b, chứng minh LF//AB và LF đi qua trung điểm BC
c, chứng minh DE//BC
Theo dõi (0) 1 Trả lời -


Chứng minh AH = AK biết tam giác ABC vuông tại A
bởi Nhat nheo
 31/05/2019
31/05/2019
Cho tam giác ABC vuông tại A. Kẻ ở ngoài tam giác , tam giác ABD vuông cân tại B và tam giác ACF vuông cân tại C. Gọi K là giao điểm của AB và CD, H là giao điểm của AC và BF. CMR :
a) AH = AK .
b) AH2 = BH.CKTheo dõi (0) 1 Trả lời -


Chứng minh BH vuông góc CN biết HM vuông góc với BC, N là giao điểm của AB và MH
bởi ngọc trang
 30/03/2019
30/03/2019
cho △ABC có góc A = 90 độ và tia phân giác BH. Kẻ HM vuông góc với BC. Gọi N là giao điểm của AB và MH. Chứng minh:
a) △ABH = △MHB
b) BH là đường trung trực của AM
c) AM //CN
d0 BH vuông góc CN
Theo dõi (0) 1 Trả lời
Bài tập SGK khác
Bài tập 9 trang 84 SBT Toán 8 Tập 2
Bài tập 10 trang 84 SBT Toán 8 Tập 2
Bài tập 12 trang 85 SBT Toán 8 Tập 2
Bài tập 13 trang 85 SBT Toán 8 Tập 2
Bài tập 14 trang 85 SBT Toán 8 Tập 2
Bài tập 15 trang 86 SBT Toán 8 Tập 2
Bài tập 16 trang 86 SBT Toán 8 Tập 2
Bài tập 2.1 trang 86 SBT Toán 8 Tập 2





