Trang chủ Toán 8

Bài tập 6 trang 9 SGK Toán 8 Tập 2

Lý thuyết

4 BT SGK

133 FAQ

Giải bài 6 tr 9 sách GK Toán 8 Tập 2

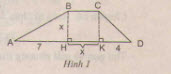
Tính diện tích của hình thang ABCD (h.1) theo x bằng hai cách:

1) Tính theo công thức \(S = BH * (BC + DA) : 2\);

2) \(S = S_{ABH} + S_{BCKH} + S_{CKD}\). Sau đó sử dụng giả thiết S = 20 để thu được hai phương trình tương đương với nhau. Trong hai phương trình ấy, có phương trình nào là phương trình bậc nhất không?

Hình 1 bài 6 trang 9 SGK Toán lớp 8 Tập 2

Hướng dẫn giải chi tiết

Gọi S là diện tích hình thang ABCD.

* Theo công thức

                    S = 

Ta có: AD = AH + HK + KD

⇒ AD = 7 + x + 4 = 11 + x

Do đó: S = 

* Ta có: S = SABH + SBCKH + SCKD. 

                 = .AH.BH + BH.HK + CK.KD

                  = .7x + x.x + x.4

                  = \(\frac{7}{2}x + x^2 + 2x\)

Vậy S = 20 ta có hai phương trình:

                   \(\frac{x(11+2x)}{2}=20\)            (1)

                   \(\frac{7}{2}x + x^2 + 2x = 20\)                (2)

-- Mod Toán 8 HỌC247

Nếu bạn thấy hướng dẫn giải Bài tập 6 trang 9 SGK Toán 8 Tập 2 HAY thì click chia sẻ 

Để luyện tập thêm dạng bài tương tự như Bài tập 6 trang 9 trong SGK các em làm thêm câu hỏi trắc nghiệm sau để cũng cố kỹ năng làm dạng bài.

  • Câu 1:

    Phương trình 2x - 3= 12 - 3x có bao nhiêu nghiệm?

    • A. 0
    • B. 1
    • C. 2
    • D. vô số nghiệm 

Được đề xuất cho bạn