Giải bài 13 tr 74 sách GK Toán 8 Tập 1
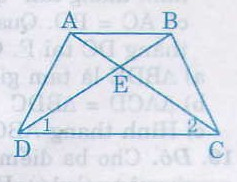
Cho hình thang cân ABCD (AB // CD), E là giao điểm của hai đường chéo. Chứng minh rằng EA = EB, EC = ED.
Hướng dẫn giải chi tiết
Do ABCD là hình thang cân nên AD = BC, AC = BC,
Xét hai tam giác ADC và BCD, ta có:
AD = BC (gt)
AC = BD (gt)
DC chung
Nên ∆ADC = ∆BCD (c.c.c)
Suy ra
Do đó tam giác ECD cân tại E, nên EC = ED
Ta lại có: AC = BD suy ra EA = EB
Chú ý: Ngoài cách chứng minh ∆ADC = ∆BCD (c.c.c) ta còn có thể chứng minh ∆ADC = ∆BCD (c.g.c) như sau:
AD = BC, , DC là cạnh chung.
-- Mod Toán 8 HỌC247
-
Bài 3.3 trang 83 sách bài tập toán 8 tập 1
bởi Nguyễn Thị Trang
13/10/2018
Bài 3.3 - Bài tập bổ sung (Sách bài tập - trang 83)
Hình thang cân ABCD (AB//CD) có \(\widehat{C}=60^0\), DB là tia phân giác của góc D. Tính các cạnh của hình thang, biết chu vi hình thang bằng 20 cm ?
Theo dõi (0) 2 Trả lời -
Bài 3.2 trang 83 sách bài tập toán 8 tập 1
bởi bala bala
13/10/2018
Bài 3.2 - Bài tập bổ sung (Sách bài tập - trang 83)
Hình thang cân ABCD (AB //CD) có hai đường chéo cắt nhau tại I, hai đường thẳng chứa các cạnh bên cắt nhau ở K. Chứng minh rằng KI là đường trung trực của hai đáy ?
Theo dõi (0) 1 Trả lời -
Bài 3.1 trang 83 sách bài tập toán 8 tập 1
bởi hành thư
29/09/2018
Bài 3.1 - Bài tập bổ sung (Sách bài tập - trang 83)Hình thang cân ABCD (AB //CD) có \(\widehat{A}=70^0\). Khẳng định nào dưới đây là đúng ?
(A) \(\widehat{C}=110^0\) (B) \(\widehat{B}=110^0\) (C) \(\widehat{C}=70^0\) (D) \(\widehat{D}=70^0\)
Theo dõi (0) 4 Trả lời
Được đề xuất cho bạn
