Phần hướng dẫn giải bài tập Hình học 8 Bài 3 Hình thang cân sẽ giúp các em nắm được phương pháp và rèn luyện kĩ năng, giải bài tập từ SGK Hình hình 8 Tập 1
-
Bài tập 11 trang 74 SGK Toán 8 Tập 1
Tính độ dài các cạnh của hình thang cân ABCD trên giấy kẻ ô vuông (h.30, độ dài cạnh ô vuông là 1cm).

-
Bài tập 12 trang 74 SGK Toán 8 Tập 1
Cho hình thang cân ABCD ( AB // CD, AB < CD). Kẻ đường cao AE, BF của hình thang. Chứng minh rằng DE = CF.
-
Bài tập 13 trang 74 SGK Toán 8 Tập 1
Cho hình thang cân ABCD (AB // CD), E là giao điểm của hai đường chéo. Chứng minh rằng EA = EB, EC = ED.
-
Bài tập 14 trang 75 SGK Toán 8 Tập 1
Đố. Trong các tứ giác ABCD và EFGH trên giấy kẻ ô vuông (h.31), tứ giác nào là hình thang cân? Vì sao?
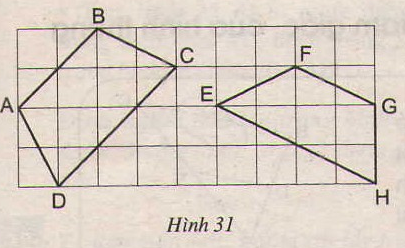
-
Bài tập 15 trang 75 SGK Toán 8 Tập 1
Cho tam giác ABC cân tại A. Trên các cạnh bên AB, AC lấy theo thứ tự các điểm D và E sao cho AD = AE.
a) Chứng minh rằng BDEC là hình thang cân.
b) Tính các góc của hình thang cân đó, biết rằng \(\widehat{A}=50^0\)
-
Bài tập 16 trang 75 SGK Toán 8 Tập 1
Cho tam giác ABC cân tại A, các đường phân giác BD, CE (D ∈ AC, E ∈ AB). Chứng minh rằng BEDC là hình thang cân có đáy nhỏ bằng cạnh bên.
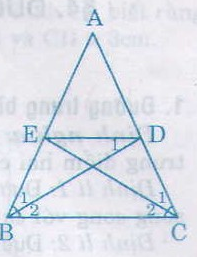
-
Bài tập 17 trang 75 SGK Toán 8 Tập 1
Hình thang ABCD (AB // CD) có \(\widehat{ACD}=\widehat{BDC}\). Chứng minh rằng ABCD là hình thang cân.
-
Bài tập 18 trang 75 SGK Toán 8 Tập 1
Chứng minh định lí "Hình thang có hai đường chéo bằng nhau là hình thang cân" qua bài toán sau: Cho hình thang ABCD (AB = CD) có AC = BD.
Qua B kẻ đường thẳng song song với AC, cắt đường thẳng DC tại E. Chứng mình rằng:
a) ∆BDE là tam giác cân.
b) \(\Delta ACD = \Delta BDC\).
c) Hình thang ABCD là hình thang cân.
-
Bài tập 19 trang 75 SGK Toán 8 Tập 1
Đố. Cho ba điểm A, D, K trên giấy kẻ ô vuông (h.32). Hãy tìm điểm thứ tư M là giao điểm của các dòng kẻ sao cho nó cùng với ba điểm đã cho là bốn đỉnh của một hình thang cân
.
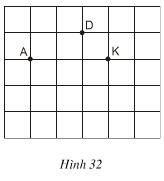
-
Bài tập 22 trang 82 SBT Toán 8 Tập 1
Hình thang cân \(ABCD\) có \(AB// CD,\) \(AB < CD.\) Kẻ các đường cao \(AH,\) \(BK.\) Chứng minh rằng \(DH = CK.\)
-
Bài tập 23 trang 82 SBT Toán 8 Tập 1
Hình thang cân \(ABCD\) có \(AB // CD,\) \(O\) là giao điểm của hai đường chéo. Chứng minh rằng \(OA=OB,\) \(OC=OD.\)
-
Bài tập 24 trang 83 SBT Toán 8 Tập 1
Cho tam giác ABC cân tại A. Trên các cạnh bên AB, AC lấy các điểm M, N sao cho BM = CN.
a. Tứ giác BMNC là hình gì ? Vì sao ?
b. Tính các góc của tứ giác BMNC biết rằng \(\widehat A = {40^0}\)
-
Bài tập 25 trang 83 SBT Toán 8 Tập 1
Cho tam giác ABC cân tại A, các đường phân giác BE, CF. Chứng minh rằng BFEC là hình thang cân có đáy nhỏ bằng cạnh bên.
-
Bài tập 26 trang 83 SBT Toán 8 Tập 1
Chứng minh rằng hình thang có hai đường chéo bằng nhau là hình thang cân.
-
Bài tập 27 trang 83 SBT Toán 8 Tập 1
Tính các góc của hình thang cân, biết một góc bằng \({50^0}\)
-
Bài tập 28 trang 83 SBT Toán 8 Tập 1
Hình thang cân ABCD có đáy nhỏ AB bằng cạnh bên AD. Chứng minh rằng CA là tia phân giác của góc C.
-
Bài tập 29 trang 83 SBT Toán 8 Tập 1
Hai đoạn thẳng AB và CD cắt nhau tại O. Biết rằng OA = OC, OB = OD. Tứ giác ACBD là hình gì ? Vì sao ?
-
Bài tập 30 trang 83 SBT Toán 8 Tập 1
Cho tam giác ABC cân tại A. Lấy điểm D trên cạnh AB, điểm E trên cạnh AC sao cho AD = AE.
a. Tứ giác BDEC là hình gì ? Vì sao ?
b. Các điểm D, E ở vị trí nào thì BD = DE = EC ?
-
Bài tập 31 trang 83 SBT Toán 8 Tập 1
Hình thang cân ABCD có O là giao điểm của hai đường thẳng chứa cạnh bên AD, BC và E là giao điểm của hai đường chéo. Chứng minh rằng OE là đường trung trực của hai đáy.
-
Bài tập 32 trang 83 SBT Toán 8 Tập 1
\(a)\) Hình thang cân \(ABCD\) có đáy nhỏ \(AB = b,\) đáy lớn \(CD = a,\) đường cao \(AH.\)Chứng minh rằng \(HD=\dfrac{a-b}{2},\) \(HC=\dfrac{a+b}{2},\) (\(a\) và \(b\) có cùng đơn vị đo)
\(b)\) Tính đường cao của hình thang cân có hai đáy \(10cm,\) \(26cm\) và cạnh bên \(17cm.\)
-
Bài tập 33 trang 83 SBT Toán 8 Tập 1
Hình thang cân ABCD có đường chéo DB vuông góc với cạnh bên BC, BD là tia phân giác của góc D. Tính chu vi của hình thang, biết BC = 3cm.
-
Bài tập 3.1 trang 83 SBT Toán 8 Tập 1
Hình thang cân \(ABCD\) \((AB // CD)\) có \(\widehat A = {70^0}\). Khẳng định nào dưới đây là đúng \(?\)
\(A.\) \(\widehat C = {110^0}\)
\(B.\) \(\widehat B = {110^0}\)
\(C.\) \(\widehat C = {70^0}\)
\(D.\) \(\widehat D = {70^0}\)
-
Bài tập 3.2 trang 84 SBT Toán 8 Tập 1
Hình thang cân ABCD (AB// CD) có hai đường chéo cắt nhau tại I, hai đường thẳng chứa các cạnh bên cắt nhau ở K. Chứng minh rằng KI là đường trung trực của hai đáy.
-
Bài tập 3.3 trang 84 SBT Toán 8 Tập 1
Hình thang cân ABCD (AB // CD) có , DB là tia phân giác của góc D. Tính các cạnh của hình thang, biết chu vi hình thang bằng 20cm.






