Giải bài 31 tr 83 sách BT Toán lớp 8 Tập 1
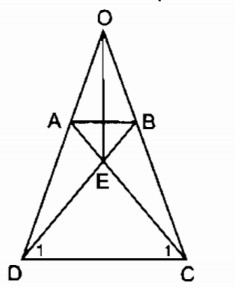
Hình thang cân ABCD có O là giao điểm của hai đường thẳng chứa cạnh bên AD, BC và E là giao điểm của hai đường chéo. Chứng minh rằng OE là đường trung trực của hai đáy.
Hướng dẫn giải chi tiết
Hướng dẫn giải
Ta sử dụng kiến thức:
+) Trong hình thang cân, hai cạnh bên bằng nhau.
+) Trong hình thang cân, hai đường chéo bằng nhau.
+) Trong tam giác cân, đường trung trực ứng với cạnh đáy đi qua đỉnh của tam giác đó.
Lời giải chi tiết
\(\eqalign{
& \widehat {ADC} = \widehat {BCD}\,\,\,\,(gt) \cr
& \Rightarrow \widehat {ODC} = \widehat {OCD} \cr} \)
⇒ ∆ OCD cân tại O
⇒ OC = OD
⇒ OA + AD = OB + BC
Mà AD = BC (tính chất hình thang cân)
⇒ OA = OB
Xét ∆ ADC và ∆ BCD :
AD = BC (chứng minh trên)
AC = BD (tính chất hình thang cân)
CD cạnh chung
Do đó: ∆ ADC = ∆ BCD (c.c.c)
\( \Rightarrow {\widehat D_1} = {\widehat C_1}\)
⇒ ∆ EDC cân tại E
⇒ EC = ED nên E thuộc đường trung trực của CD
OC = OD nên O thuộc đường trung trực của CD
E≢ O. Vậy OE là đường trung trực của CD.
BD = AC (chứng minh trên)
⇒ EB + ED = EA + EC mà ED = EC
⇒ EB = EA nên E thuộc đường trung trực AB
E≢ O. Vậy OE là đường trung trực của AB.
-- Mod Toán 8 HỌC247
-
Chứn minh chu vi tam giác IJK = OA+OB+OC
bởi Trieu Tien
31/05/2019
O là 1 điểm tùy ý nằm trong tam giác đều ABC . Kẻ OI//AB ( I thuộc AC ) , OJ//BC ( J thuộc AB ) , OK//AC ( K thuộc BC )
CMR : Chu vi tam giác IJK = OA+OB+OC
Theo dõi (0) 1 Trả lời -
Cho ABCD là hình thang cân đáy AB và CD
Qua B kẻ đường thẳng song song AC cắt đường thẳng DC tại E
a)Cm:Tam giác DBE cân
b)kẻ BK vuông DC tại K và góc BDC=45 độ
cm:BK=1/2 DE
Theo dõi (0) 1 Trả lời -
1. Cho tam giác ABCD cân tại A . Trên các cạnh bên AB , AC lấy theo thứ tự các điểm D và E sao cho AD=AE.
a) Chứng minh rằng BDEC là hình thang cân .
b) Tính các góc của hình thang cân đó , biết rằng góc A = 50 độ
2. Cho tam giác ABCD cân tại A , các đường phân giác BD, CE ( D thuộc AC , E thuộc AB ) .
Chứng minh rằng BEDC là hình thang cân có đáy nhỏ = cạnh bên .
3 . Hình thang ABCD ( AB // CD ) có góc ACD = góc BDC . Chứng minh rằng ABCD là hình thang cân
Theo dõi (0) 1 Trả lời -
Chứng minh tứ giác MNPQ là hình thang cân
bởi Goc pho
31/05/2019
cho hình thang MNPQ ( MN//PQ) có góc MPQ = góc NQP . chứng minh : tứ giác MNPQ là hình thang cân
CÁC BẠN ƠI GIÚP MÌNH VỚI
Theo dõi (0) 1 Trả lời -
Chứng minh BF vuông góc với CD
bởi minh thuận
31/05/2019
Cho hình thang cân ABCD (ab//cd). E là trung điểm của BC, qua E kể đường thẳng song song với AD cắt CD ở F. Chứng minh BF vuông góc với CD.
Theo dõi (0) 1 Trả lời -
Cho tam giác ABC cân tại A Trên tia đối của tia BA lấy D trên tia đối của tia CA lấy E sao cho BD = CE. 1.Chứng minh rằng tứ giác BCED là hình thang cân. 2. Tin các goc của hình thang trên neu goc BAC = 30
Theo dõi (0) 1 Trả lời
