Giải bài 18 tr 75 sách GK Toán 8 Tập 1
Chứng minh định lí "Hình thang có hai đường chéo bằng nhau là hình thang cân" qua bài toán sau: Cho hình thang ABCD (AB = CD) có AC = BD.
Qua B kẻ đường thẳng song song với AC, cắt đường thẳng DC tại E. Chứng mình rằng:
a) ∆BDE là tam giác cân.
b) \(\Delta ACD = \Delta BDC\).
c) Hình thang ABCD là hình thang cân.
Hướng dẫn giải chi tiết
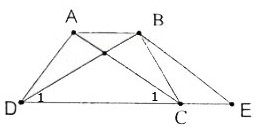
a) \(E\) thuộc đường thẳng \(DC\) nên \(CE // AB.\)
Hình thang \(ABEC\; (AB // CE)\) có hai cạnh bên \(AC, BE\) song song (giả thiết) \( \Rightarrow AC = BE\) (1) (nếu một hình thang có hai cạnh bên song song thì hai cạnh bên bằng nhau )
Lại có: \(AC = BD\) (giả thiết) (2)
Từ (1) và (2) suy ra \(BE = BD\) \( \Rightarrow \Delta BED\) cân tại \(B\) (dấu hiệu nhận biết tam giác cân).
b) Ta có \(AC{\rm{ }}//{\rm{ }}BE \Rightarrow \widehat {{C_1}} = \widehat E\) (2 góc đồng vị) (3)
\(∆BDE\) cân tại \(B\) (chứng minh trên) \( \Rightarrow \widehat {{D_1}} = \widehat E\) (4)
Từ (3) và (4) \( \Rightarrow \widehat {{D_1}} = \widehat {{C_1}}\)
Xét \(∆ACD\) và \( ∆BDC\) có:
+) \(AC = BD\) (giả thiết)
+) \(\widehat {{C_1}} = \widehat {{D_1}}\) (chứng minh trên)
+) \(CD\) chung
Suy ra \(∆ACD = ∆BDC\) (c.g.c)
c) Ta có: \(∆ACD = ∆BDC\) (chứng minh trên)
\( \Rightarrow \widehat {A{\rm{D}}C} = \widehat {BCD}\) (\(2\) góc tương ứng)
Hình thang \(ABCD\) có hai góc kề một đáy bằng nhau nên là hình thang cân.
-- Mod Toán 8 HỌC247
-


Hai đoạn thẳng AB và CD cắt nhau tại O. Biết rằng OA = OC, OB = OD. Tứ giác ACBD là hình gì ? Vì sao?
Theo dõi (0) 1 Trả lời -


Chứng minh F, O, G thẳng hàng biết hình thang cân ABCD có O là giao điểm của 2 đường chéo AC và BD
bởi Nguyễn Tiểu Ly
 31/05/2019
31/05/2019
Cho hình thang cân ABCD, gọi O là giao điểm 2 đường chéo AC và BD ; F là trung điểm của AB, G là trung điểm của CD. C/m 3 điểm F, O, G thẳng hàng.
Theo dõi (0) 1 Trả lời -


Chứng minh M O, I thẳng hàng biết hình thang ABCD có AB//CD và AD cắt BC tại I
bởi Nguyễn Thị Thanh
 31/05/2019
31/05/2019
Cho hinh thang can ABCD coAB//CD va AD cat BC tai I, O la giao diem cua AC va BD; M la trung diem cua AB. c.m M, O, I thang hang
Theo dõi (0) 1 Trả lời -


Chứng minh OM = ON biết MH cắt NP tại O
bởi trang lan
 31/05/2019
31/05/2019
Cho ΔABC, kẻ AH ⊥ BC. Gọi M,N,P thứ tự là trung điểm AB,AC,BC
a) Chứng minh MNPH là hình thang cân
b) MH cắt NP tại O. Chứng minh OM = ON
Theo dõi (0) 1 Trả lời -


cho hình thang cân ABCD (AB//CD) góc D = 50 độ . tính các góc của hình thang cân
Theo dõi (0) 1 Trả lời -


Cho hình thang ABCD cân có
\(\widehat{C}=60 độ\) ,đáy nhỏ AB=AD. Biết chu vi hình thang là 20cm. Tính chiều cao và diện tích hình thang
Theo dõi (0) 1 Trả lời
Bài tập SGK khác
Bài tập 16 trang 75 SGK Toán 8 Tập 1
Bài tập 17 trang 75 SGK Toán 8 Tập 1
Bài tập 19 trang 75 SGK Toán 8 Tập 1
Bài tập 22 trang 82 SBT Toán 8 Tập 1
Bài tập 23 trang 82 SBT Toán 8 Tập 1
Bài tập 24 trang 83 SBT Toán 8 Tập 1
Bài tập 25 trang 83 SBT Toán 8 Tập 1
Bài tập 26 trang 83 SBT Toán 8 Tập 1
Bài tập 27 trang 83 SBT Toán 8 Tập 1
Bài tập 28 trang 83 SBT Toán 8 Tập 1
Bài tập 29 trang 83 SBT Toán 8 Tập 1
Bài tập 30 trang 83 SBT Toán 8 Tập 1
Bài tập 31 trang 83 SBT Toán 8 Tập 1
Bài tập 32 trang 83 SBT Toán 8 Tập 1
Bài tập 33 trang 83 SBT Toán 8 Tập 1
Bài tập 3.1 trang 83 SBT Toán 8 Tập 1





