Giải bài 34 tr 123 sách GK Toán lớp 7 Tập 1
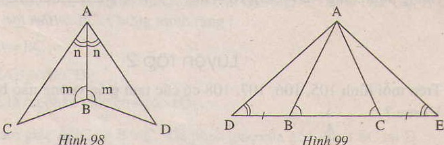
Trên mỗi hình 98,99 có tam giác nào bằng nhau? Vì sao?
Hướng dẫn giải chi tiết
Xem hình 98)
∆ABC và ∆ABD có:
=
(gt)
AB là cạnh chung.
=
(gt)
Nên ∆ABC=∆ABD(g.c.g)
Xem hình 99)
Ta có:
+
=1800 (Hai góc kề bù).
+
=1800 (Hai góc kề bù)
Mà =
(gt)
Nên =
* ∆ABD và ∆ACE có:
=
(cmt)
BD=EC(gt)
=
(gt)
Nên ∆ABD=∆ACE(g.c.g)
* ∆ADC và ∆AEB có:
=
(gt)
=
(gt)
DC=EB
Nên ∆ADC=∆AEB(g.c.g)
-- Mod Toán 7 HỌC247
-


Cho tam giác ABC vuông tại A. Kẻ AH vuông góc với BC sao cho H thuộc BC. Tim góc bằng góc B.
bởi Trinh Heo
 19/03/2020
Cho tam giác ABC vuông tại A. Kẻ AH vuông góc với BC sao cho H thuộc BC. Tim góc bằng góc B.Theo dõi (0) 3 Trả lời
19/03/2020
Cho tam giác ABC vuông tại A. Kẻ AH vuông góc với BC sao cho H thuộc BC. Tim góc bằng góc B.Theo dõi (0) 3 Trả lời -


Bài tập chương Tam giác
bởi SUNEK
 17/03/2020
Bài 2
17/03/2020
Bài 2 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


Cho góc nhọn xOy có tia phân giác Ot. Lấy điểm A trên tia Ox, điểm B trên tia Oy sao cho OA = OB. Lấy điểm C bất kì trên tia Ot sao cho OC>OA. Chứng minh ∆AOC = ∆BOC và CO là tia phân giác của góc ACB.
bởi Đặng Phong
 13/03/2020
Giúp mk vs!! mình đang cần gấp!Theo dõi (0) 1 Trả lời
13/03/2020
Giúp mk vs!! mình đang cần gấp!Theo dõi (0) 1 Trả lời -


Tìm x, y, z biết: x-y+z=36 và x/5=y/6=z/7
bởi Đặng Phong
 12/03/2020
Mình đang cần! Cảm ơn!
12/03/2020
Mình đang cần! Cảm ơn! Theo dõi (0) 3 Trả lời
Theo dõi (0) 3 Trả lời -


Tìm x, biết 3/4-(1/2:x)=2/3
bởi Đặng Phong
 12/03/2020
Mình đang cần gấp!Cảm ơn!!
12/03/2020
Mình đang cần gấp!Cảm ơn!! Theo dõi (0) 3 Trả lời
Theo dõi (0) 3 Trả lời -


Cho tam giác ABC có AB=AC. Trên cạnh AB lấy điểm E, trên cạnh AC lấy điểm D sao cho AE=AD. Gọi F là giao điểm của BD và CE, H là trung điểm của BC. Chứng minh rằng ∆ADB=∆AEC
bởi Không Tồn Tại
 03/03/2020
03/03/2020
 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


Cho tam giác ABD, O là trung điểm BD. Lấy điểm M,C,N sao cho B,O,D lần lượt là trung điểm của AM,AC,AN. Chứng minh: BC=AD và BC //AD M,C,N thẳng hàng
bởi Sỹ Xuân
 21/02/2020
Cho tam giác ABD, O là trung điểm BD. Lấy điểm M,C,N sao cho B,O,D lần lượt là trung điểm của AM,AC,AN. Chứng minh: a) BC=AD và BC //AD b) t/giác ABD = t/giác BMC c) MC//BD d) 3 điểm M,C,N thẳng hàngTheo dõi (0) 0 Trả lời
21/02/2020
Cho tam giác ABD, O là trung điểm BD. Lấy điểm M,C,N sao cho B,O,D lần lượt là trung điểm của AM,AC,AN. Chứng minh: a) BC=AD và BC //AD b) t/giác ABD = t/giác BMC c) MC//BD d) 3 điểm M,C,N thẳng hàngTheo dõi (0) 0 Trả lời -


Cho tam giác ABC, vẽ góc DAB=60 độ, AD=AB( AD và AC khác phía đối với AB), vẽ góc CAB= 60 độ, AE=AC( AE và AB khác phía đối với AC). DC cắt BE tại K. Chứng minh góc DAC=góc BAE
bởi Sỹ Xuân
 21/02/2020
Cho tam giác ABC, vẽ góc DAB=60 độ, AD=AB( AD và AC khác phía đối với AB), vẽ góc CAB= 60 độ, AE=AC( AE và AB khác phía đối với AC). DC cắt BE tại K a) chứng minh góc DAC=góc BAE b) Chứng minh DC=BE c) tính góc BKCTheo dõi (0) 0 Trả lời
21/02/2020
Cho tam giác ABC, vẽ góc DAB=60 độ, AD=AB( AD và AC khác phía đối với AB), vẽ góc CAB= 60 độ, AE=AC( AE và AB khác phía đối với AC). DC cắt BE tại K a) chứng minh góc DAC=góc BAE b) Chứng minh DC=BE c) tính góc BKCTheo dõi (0) 0 Trả lời -


Cho tam giác ABC cân tại A, D là trung điểm của AC. Từ A kẻ đường thẳng vuông góc với BD, cắt cạnh BC tại E. Chứng minh: AE=2DE
bởi Tuan Nguyen
 14/02/2020
14/02/2020
 Theo dõi (1) 2 Trả lời
Theo dõi (1) 2 Trả lời -


Cho tam giác ABC cân tại A. Điểm D thuộc cạnhAB, điểm E thuộc canh AC sao cho AD bằng AE.Gọi K là Giao điểm của BE và CD. Chứng minh: a/ BE bằng CD.
bởi Trang Nguyễn Minh
 13/02/2020
Cho tam giác ABC cân tại A. Điểm D thuộc cạnhAB, điểm E thuộc canh AC sao cho AD bằng AE.Gọi K là Giao điểm của BE và CD. Chứng minh: a/ BE bằng CD. b/ Tam giác KBD bằng tam giác KCE c/ AK là phân giác của góc A. d/ tam giác KBC cân. ( cần lời giải)Theo dõi (0) 0 Trả lời
13/02/2020
Cho tam giác ABC cân tại A. Điểm D thuộc cạnhAB, điểm E thuộc canh AC sao cho AD bằng AE.Gọi K là Giao điểm của BE và CD. Chứng minh: a/ BE bằng CD. b/ Tam giác KBD bằng tam giác KCE c/ AK là phân giác của góc A. d/ tam giác KBC cân. ( cần lời giải)Theo dõi (0) 0 Trả lời -


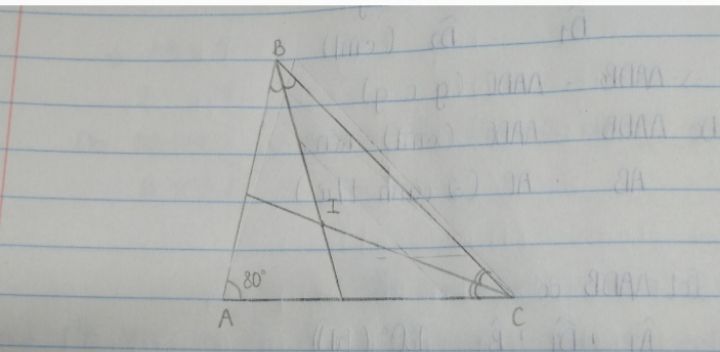
Cho tam giác ABC có góc A =80°, tia phân giác của góc B và góc C cắt nhau tại I. Tính góc BIC
bởi Như Vũ
 10/01/2020
10/01/2020
 Theo dõi (0) 2 Trả lời
Theo dõi (0) 2 Trả lời -


Cách chứng minh 1 điểm là trung điểm của đoạn thẳng
bởi Nghi Ph
 25/12/2019
25/12/2019
Cách chứng minh 1 điểm là trung điểm của đoạn thẳng
Theo dõi (0) 1 Trả lời -


Chứng minh tam giác AED = ACD biết tam giác ABC có D là trung điểm của AE, E là trung điểm của AC
bởi Nghi Ph
 25/12/2019
25/12/2019
Cho tam giác ABC, D là trung điểm của AE, E là trung điểm của AC. Trên tia đối của tia ED lấy điểm F sao cho EF = ED.
a. Chứng minh tam giác AED = ACD
b. Chứng minh CF song song ABc. Chứng minh DF = BC
Theo dõi (0) 3 Trả lời -

 giúp mình vớiTheo dõi (0) 4 Trả lời
giúp mình vớiTheo dõi (0) 4 Trả lời -


Chứng minh tam giác ADB=tam giác MDC biết tam giác có AB=AC, tia phân giác của góc ABC cắt BC tại D
bởi Phung Hoa Phung Hoa
 22/12/2019
Tổng 3trường hợp của tam giác
22/12/2019
Tổng 3trường hợp của tam giác Theo dõi (0) 2 Trả lời
Theo dõi (0) 2 Trả lời
Bài tập SGK khác
Bài tập 33 trang 123 SGK Toán 7 Tập 1
Bài tập 35 trang 123 SGK Toán 7 Tập 1
Bài tập 36 trang 123 SGK Toán 7 Tập 1
Bài tập 37 trang 123 SGK Toán 7 Tập 1
Bài tập 49 trang 144 SBT Toán 7 Tập 1
Bài tập 50 trang 144 SBT Toán 7 Tập 1
Bài tập 51 trang 144 SBT Toán 7 Tập 1
Bài tập 52 trang 144 SBT Toán 7 Tập 1
Bài tập 53 trang 144 SBT Toán 7 Tập 1
Bài tập 54 trang 144 SBT Toán 7 Tập 1
Bài tập 55 trang 145 SBT Toán 7 Tập 1
Bài tập 56 trang 145 SBT Toán 7 Tập 1
Bài tập 57 trang 145 SBT Toán 7 Tập 1
Bài tập 57 trang 145 SBT Toán 7 Tập 1
Bài tập 59 trang 145 SBT Toán 7 Tập 1
Bài tập 60 trang 145 SBT Toán 7 Tập 1
Bài tập 61 trang 145 SBT Toán 7 Tập 1
Bài tập 62 trang 145 SBT Toán 7 Tập 1
Bài tập 63 trang 146 SBT Toán 7 Tập 1
Bài tập 64 trang 146 SBT Toán 7 Tập 1





