Giải bài tập Toán 11 Kết nối tri thức Bài 16: Giới hạn của hàm số

Trong Thuyết tương đối của Einstein, khối lượng của vật chuyển động với vận tốc v cho bởi công thức

$$m = \frac{{{m_0}}}{{\sqrt {1 - \frac{{{v^2}}}{{{c^2}}}} }}$$

trong đó m₀ là khối lượng của vật khi nó đứng yên, c là vận tốc ánh sáng. Chuyện gì xảy ra với khối lượng của vật khi vận tốc của vật gần với vận tốc ánh sáng?

Cho hàm số $f\left( x \right) = \frac{{4 - {x^2}}}{{x - 2}}$.

a) Tìm tập xác định của hàm số f(x).

b) Cho dãy số ${x_n} = \frac{{2n + 1}}{n}$. Rút gọn f(x_n) và tính giới hạn của dãy (u_n) với u_n = f(x_n).

c) Với dãy số (x_n) bất kì sao cho x_n ≠ 2 và x_n ⟶ 2, tính f(x_n) và tìm $\mathop {\lim }\limits_{n \to  + \infty } f\left( {{x_n}} \right)$.

Tính $\mathop {\lim }\limits_{x \to 1} \frac{{x - 1}}{{\sqrt x  - 1}}$.

Cho hàm số $f\left( x \right) = \frac{{\left| {x - 1} \right|}}{{x - 1}}$

a) Cho ${x_n} = \frac{n}{{n + 1}}$ và $x_n^\prime  = \frac{{n + 1}}{n}$. Tính ${y_n} = f\left( {{x_n}} \right)$ và $y_n^\prime  = f\left( {{{x'}_n}} \right)$

b) Tìm giới hạn của các dãy số $\left( {{y_n}} \right)$ và $\left( {{y'_n}} \right)$

c) Cho các dãy số $\left( {{x_n}} \right)$ và $\left( {{x'_n}} \right)$ bất kì sao cho x_n < 1 < x′_n và x_n→1,x′_n→1, tính $\mathop {{\rm{lim}}}\limits_{n \to  + \infty } f\left( {{x_n}} \right)$ và $\mathop {{\rm{lim}}}\limits_{n \to  + \infty } f\left( {{x'_n}} \right)$

Cho hàm số $f\left( x \right) = \left\{ \begin{array}{l} - x,x < 0\\ \sqrt x ,x \ge 0 \end{array} \right.$

Tính $\mathop {{\rm{lim}}}\limits_{x \to {0^ + }} f\left( x \right),\:\:\:\:\mathop {{\rm{lim}}}\limits_{x \to {0^ - }} \:f\left( x \right)$ và $\mathop {{\rm{lim}}}\limits_{x \to 0} \:f\left( x \right)$

Cho hàm số $f\left( x \right) = 1 + \frac{2}{{x - 1}}$ có đồ thị như Hình 5.4.

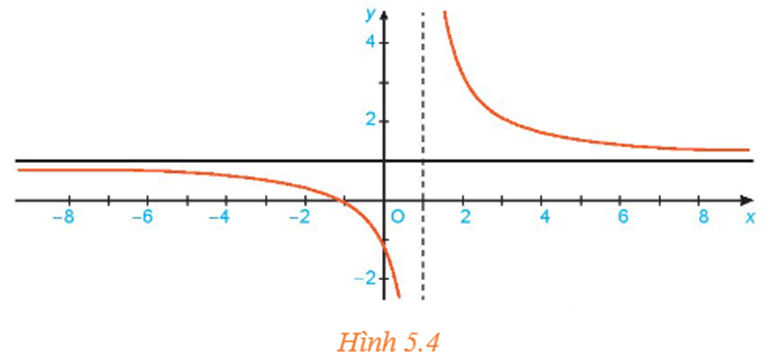
Giả sử (x_n) là dãy số sao cho x_n > 1, x_n ⟶ +∞. Tính f(x_n) và $\mathop {\lim }\limits_{n \to  + \infty } f\left( {{x_n}} \right)$.

Tính: $\mathop {{\rm{lim}}}\limits_{x \to  + \infty } \frac{{\sqrt {{x^2} + 2} }}{{x + 1}}$.

Cho tam giác OAB với A = (a; 0) và B = (0; 1) như Hình 5.5. Đường cao OH có độ dài là h.

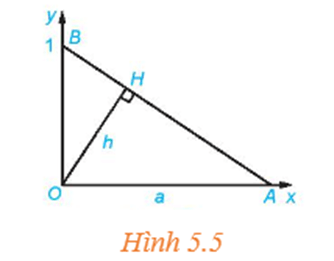
a) Tính h theo a.

b) Khi điểm A dịch chuyển về O, điểm H thay đổi thế nào? Tại sao?

c) Khi A dịch chuyển ra vô cực theo chiều dương của trục Ox, điểm H thay đổi thế nào? Tại sao?

Xét hàm số $f\left( x \right) = \frac{1}{{{x^2}}}$ có đồ thị như Hình 5.6.

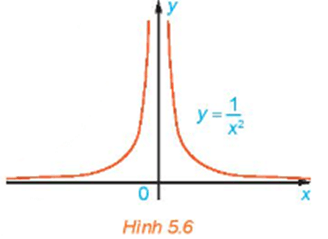
Cho ${x_n} = \frac{1}{n}$, chứng tỏ rằng f(x_n) ⟶ +∞.

Cho hàm số $f\left( x \right) = \frac{1}{{x - 1}}$. Với các dãy số (x_n) và (x'_n) cho bởi ${x_n} = 1 + \frac{1}{n},{{x'}_n} = 1 - \frac{1}{n}$, tính $\mathop {\lim }\limits_{n \to  + \infty } f\left( {{x_n}} \right),\mathop {\lim }\limits_{n \to  + \infty } f\left( {x{'_n}} \right)$.

Tính các giới hạn sau:

a) $\mathop {{\rm{lim}}}\limits_{x \to 0} \frac{2}{{\left| x \right|}}$.

b) $\mathop {{\rm{lim}}}\limits_{x \to {2^ - }} \frac{1}{{\sqrt {2 - x} }}$

Tính $\mathop {{\rm{lim}}}\limits_{x \to {2^ + }} \frac{{2x - 1}}{{x - 2}}$ và $\mathop {{\rm{lim}}}\limits_{x \to {2^ - }} \frac{{2x - 1}}{{x - 2}}$.

Cho hai hàm số $f\left( x \right) = \frac{{{x^2} - 1}}{{x - 1}}$ và g(x) = x + 1. Khẳng định nào sau đây là đúng?

a) f(x) = g(x);

b) $\mathop {\lim }\limits_{x \to 1} f\left( x \right) = \mathop {\lim }\limits_{x \to 1} g\left( x \right)$.

Tính các giới hạn sau:

a) $\mathop {\lim }\limits_{x \to 0} \frac{{{{\left( {x + 2} \right)}^2} - 4}}{x}$;

b) $\mathop {\lim }\limits_{x \to 0} \frac{{\sqrt {{x^2} + 9}  - 3}}{{{x^2}}}$.

Cho hàm số $H\left( t \right) = \left\{ \begin{array}{l} 1,\,t < 0,\\ 0,\,t \ge 0. \end{array} \right.$  (hàm Heaviside, thường được dùng để mô tả việc chuyển trạng thái tắt/mở của dòng điện tại thời điểm t = 0).

Tính $\mathop {{\rm{lim}}}\limits_{t \to {0^ + }} H\left( t \right)$ và $\mathop {{\rm{lim}}}\limits_{t \to 0} \:H\left( t \right).$

Tính các giới hạn một bên:

a) $\mathop {\lim }\limits_{x \to {1^ + }} \frac{{x - 2}}{{x - 1}}$;

b) $\mathop {\lim }\limits_{x \to {4^ - }} \frac{{{x^2} - x + 1}}{{4 - x}}$.

Cho hàm số $g\left( x \right) = \frac{{{x^2} - 5x + 6}}{{\left| {x - 2} \right|}}$

Tìm $\mathop {{\rm{lim}}}\limits_{x \to {2^ + }}g\left( x \right)$ và $\mathop {{\rm{lim}}}\limits_{x \to 2^-} \:g\left(x \right).$

Tính các giới hạn sau:

a) $\mathop {\lim }\limits_{x \to  + \infty } \frac{{1 - 2x}}{{\sqrt {{x^2} + 1} }}$;

b) $\mathop {\lim }\limits_{x \to  + \infty } \left( {\sqrt {{x^2} + x + 2}  - x} \right)$.

Cho hàm số $f\left( x \right) = \frac{2}{{\left( {x - 1} \right)\left( {x - 2} \right)}}$.

Tính $\mathop {{\rm{lim}}}\limits_{x \to {2^ + }}f\left( x \right)$ và $\mathop {{\rm{lim}}}\limits_{x \to 2^-} \:f\left(x \right).$

Cho hàm số $f\left( x \right) = \left\{ \begin{array}{l}x\;\;\;khi\;x > 1\\2\;\;\;khi\;x = 1\\1\;\;\;khi\;x < 1\end{array} \right.$. Hàm số f(x) có giới hạn khi $x \to 1$ không?

Tính các giới hạn sau:

a) $\mathop {\lim }\limits_{x \to 2} \frac{{\sqrt {4x + 1} - 3}}{{x - 2}};$

b) $\mathop {\lim }\limits_{x \to 1} \frac{{{x^3} + {x^2} + x - 3}}{{{x^3} - 1}};$

c) $\mathop {\lim }\limits_{x \to {2^ + }} \frac{{{x^2} - 5x + 6}}{{{{\left( {x - 2} \right)}^2}}};$

d) $\mathop {\lim }\limits_{x \to {0^ - }} \frac{{{x^2} + x - 2}}{x}.$

Tìm a để hàm số $f\left( x \right) = \left\{ \begin{array}{l}{x^2} + ax\;\;khi\;x > 3\\3{x^2} + 1\;\;\;khi\;x \le 3\end{array} \right.$ có giới hạn khi $x \to 3$?

Tìm các số thực a và b sao cho $\mathop {\lim }\limits_{x \to 1} \frac{{2{x^2} - ax + 1}}{{{x^2} - 3x + 1}} = b$?

Cho hàm số $f\left( x \right) = \frac{{\sqrt {{x^2} - x + 2} }}{x}$. Tính

a) $\mathop {\lim }\limits_{x \to + \infty } f\left( x \right);$

b) $\mathop {\lim }\limits_{x \to - \infty } f\left( x \right);$

Tìm giới hạn $\mathop {\lim }\limits_{x \to + \infty } \left( {1 - x} \right)\left( {1 - {x^2}} \right)\left( {1 - {x^3}} \right)$?

Cho hàm số $g\left( x \right) = \sqrt {{x^2} + 2x} - \sqrt {{x^2} - 1} - 2m$ với m là tham số. Biết $\mathop {\lim }\limits_{x \to + \infty } g\left( x \right) = 0$, tìm giá trị của m?

Cho m là một số thực. Biết $\mathop {\lim }\limits_{x \to - \infty } \left[ {\left( {m - x} \right)\left( {mx + 1} \right)} \right] = - \infty$. Xác định dấu của m?

Cho hàm số $f\left( x \right) = \frac{{{{\sin }^2}x}}{{{x^2}}}$. Chứng minh rằng $\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = 0$?

Một đơn vị sản xuất hàng thủ công ước tính chi phí để sản xuất x đơn vị sản phẩm là $C\left( x \right) = 2x + 55$ (triệu đồng).

a) Tìm hàm số f(x) biểu thị chi phí trung bình để sản xuất mỗi đơn vị sản phẩm.

b) Tính $\mathop {\lim }\limits_{x \to + \infty } f\left( x \right)$. Giới hạn này có ý nghĩa gì?