Hoạt động 4 trang 115 SGK Toán 11 Kết nối tri thức tập 1
Xét hàm số \(f\left( x \right) = \frac{1}{{{x^2}}}\) có đồ thị như Hình 5.6.
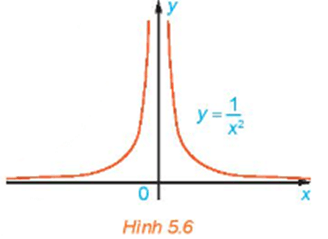
Cho \({x_n} = \frac{1}{n}\), chứng tỏ rằng f(xn) ⟶ +∞.
Hướng dẫn giải chi tiết Hoạt động 4
Phương pháp giải
Giả sử (a, b) là một khoảng chứa \(x_0\) và hàm số \(y = f(x)\) xác định trên khoảng (a, b)\(\backslash \{x_0\}\).
- Ta nói hàm số \(y = f(x)\) có giới hạn \(+\infty\) khi \(x\to x_0\) nếu với dãy số (\(x_n\)) bất kì, \(x_n\in (a, b)\backslash \{x_0\}\) và \(x_n \to x_0\), ta có \(f(x_n) \to +\infty\).
Lời giải chi tiết
Ta có: \({x_n} = \frac{1}{n}\), do đó \(f\left( {{x_n}} \right) = \frac{1}{{x_n^2}} = \frac{1}{{{{\left( {\frac{1}{n}} \right)}^2}}} = {n^2}\).
Vì n ⟶ +∞ nên \({x_n} = \frac{1}{n}\) và f(xn) ⟶ +∞.
-- Mod Toán 11 HỌC247
Chưa có câu hỏi nào. Em hãy trở thành người đầu tiên đặt câu hỏi.
Bài tập SGK khác
Luyện tập 3 trang 115 SGK Toán 11 Kết nối tri thức tập 1 - KNTT
Vận dụng trang 115 SGK Toán 11 Kết nối tri thức tập 1 - KNTT
Hoạt động 5 trang 116 SGK Toán 11 Kết nối tri thức tập 1 - KNTT
Luyện tập 4 trang 116 SGK Toán 11 Kết nối tri thức tập 1 - KNTT
Luyện tập 5 trang 118 SGK Toán 11 Kết nối tri thức tập 1 - KNTT
Giải Bài 5.7 trang 118 SGK Toán 11 Kết nối tri thức tập 1 - KNTT
Giải Bài 5.8 trang 118 SGK Toán 11 Kết nối tri thức tập 1 - KNTT
Giải Bài 5.9 trang 118 SGK Toán 11 Kết nối tri thức tập 1 - KNTT
Giải Bài 5.10 trang 118 SGK Toán 11 Kết nối tri thức tập 1 - KNTT
Giải Bài 5.11 trang 118 SGK Toán 11 Kết nối tri thức tập 1 - KNTT
Giải Bài 5.12 trang 118 SGK Toán 11 Kết nối tri thức tập 1 - KNTT
Giải Bài 5.13 trang 118 SGK Toán 11 Kết nối tri thức tập 1 - KNTT
Bài tập 5.11 trang 83 SBT Toán 11 Tập 1 Kết nối tri thức - KNTT
Bài tập 5.12 trang 83 SBT Toán 11 Tập 1 Kết nối tri thức - KNTT
Bài tập 5.13 trang 83 SBT Toán 11 Tập 1 Kết nối tri thức - KNTT
Bài tập 5.14 trang 83 SBT Toán 11 Tập 1 Kết nối tri thức - KNTT
Bài tập 5.15 trang 83 SBT Toán 11 Tập 1 Kết nối tri thức - KNTT
Bài tập 5.16 trang 83 SBT Toán 11 Tập 1 Kết nối tri thức - KNTT
Bài tập 5.17 trang 83 SBT Toán 11 Tập 1 Kết nối tri thức - KNTT
Bài tập 5.18 trang 83 SBT Toán 11 Tập 1 Kết nối tri thức - KNTT
Bài tập 5.19 trang 83 SBT Toán 11 Tập 1 Kết nối tri thức - KNTT
Bài tập 5.20 trang 83 SBT Toán 11 Tập 1 Kết nối tri thức - KNTT





