HOC247 mời các em tham khảo nội dung tóm tắt của bài học Giới hạn của hàm số môn Toán lớp 11 Kết Nối Tri Thức sau đây. Thông qua bài này, các em có thể nhận biết giới hạn hữu hạn của hàm số tại một điểm, giới hạn hữu hạn của hàm số tại vô cực, giới hạn vô cực của hàm số tại một điểm. Và từ đó vận dụng kiến thức vào bài tập tính giới hạn của hàm số mà các em có thể xem ở phần Bài tập minh họa phía dưới đây.
Tóm tắt lý thuyết
1.1. Giới hạn hữu hạn của hàm số tại một điểm
a) Khái niệm giới hạn tại một điểm
|
Giả sử (a, b) là một khoảng chứa điểm \(x_0\) và hàm số \(y = f(x)\) xác định trên khoảng (a, b), có thể trừ điểm \(x_0\). Ta nói hàm số \(y = f(x)\) có giới hạn là số L khi x dần tới \(x_0\) nếu với dãy số (\(x_n\)) bất kì, \(x_n\in (a, b)\) ,\(x_n \ne x_0\) và \(x_n \to x_0\), ta có \(f(x_n) \to L\). Kí hiệu: \(\lim \limits_{x \to {x_0} }f(x) = L\) hay \(f(x) \to L\) khi \(x_n \to x_0\). |
Tương tự đối với dãy số, ta có các quy tắc tính giới hạn của hàm số tại một điểm như sau:
|
- Nếu \(\mathop {\lim }\limits_{x \to + \infty } {f(x)} = L, \mathop {\lim }\limits_{x \to + \infty } {g(x)} =M\) thì + \(\mathop {\lim }\limits_{x \to + \infty } [f(x) + g(x)] = L + M\) + \(\mathop {\lim }\limits_{x \to + \infty } [f(x) - g(x)] = L - M\) + \(\mathop {\lim }\limits_{x \to + \infty } [f(x).g(x)] = L.M\) + \(\mathop {\lim }\limits_{x \to + \infty } \frac{{{f(x)}}}{{{g(x)}}} = \frac{L}{M}{\rm{ (}}M \ne 0)\) - Nếu \({f(x)} \ge 0\) với mọi \(x\in (a, b)\backslash\{x_0\}\) và \(\mathop {\lim }\limits_{x \to + \infty } {f(x)} = L\) thì \(L\ge 0\) và \(\mathop {\lim }\limits_{x \to + \infty } \sqrt {{f(x)}} = \sqrt L\) |
b) Khái niệm giới hạn một bên
|
- Cho hàm số \(y = f(x)\) xác định trên \(({x_0};b)\). Số \(L\) gọi là giới hạn bên phải của hàm số \(y = f(x)\) khi \(x \to {x_0}\) nếu với mọi dãy \(({x_n})\) thỏa mãn \({x_0} < {x_n} < b\) và \({x_n} \to {x_0}\) thì ta có: \(f({x_n}) \to L\). Kí hiệu: \(\mathop {\lim }\limits_{x \to x_0^ + } f(x) = L\). - Cho hàm số \(y = f(x)\) xác định trên \((a;{x_0})\). Số \(L\) gọi là giới hạn bên trái của hàm số \(y = f(x)\) khi \(x \to {x_0}\) nếu với mọi dãy \(({x_n})\) thỏa mãn \(a < {x_n} < {x_0}\) và \({x_n} \to {x_0}\) thì ta có: \(f({x_n}) \to L\). Kí hiệu: \(\mathop {\lim }\limits_{x \to x_0^ - } f(x) = L\). |
Chú ý:
1.2. Giới hạn hữu hạn của hàm số tại vô cực
|
- Cho hàm số \(y = f(x)\) xác định trên khoảng \((a; +\infty)\). Ta nói hàm số \(y = f(x)\) có giới hạn là số L khi \(x \to +\infty\) nếu với dãy số (\(x_n\)) bất kì, \(x_n>a\) và \(x_n \to +\infty\), ta có \(f(x_n) \to L\). Kí hiệu: \(\lim \limits_{x \to +\infty }f(x) = L\) hay \(f(x) \to L\) khi \(x \to +\infty\). - Cho hàm số \(y = f(x)\) xác định trên khoảng \((-\infty; b)\). Ta nói hàm số \(y = f(x)\) có giới hạn là số L khi \(x \to -\infty\) nếu với dãy số (\(x_n\)) bất kì, \(x_n>a\) và \(x_n \to -\infty\), ta có \(f(x_n) \to L\). Kí hiệu: \(\lim \limits_{x \to -\infty }f(x) = L\) hay \(f(x) \to L\) khi \(x \to -\infty\). |
Nhận xét:
+ Các quy tắc tính giới hạn hữu hạn tại một điểm cũng đúng cho giới hạn hữu hạn tại vô cực.
+ \(\mathop {\lim }\limits_{x \to + \infty } c = c\); \(\mathop {\lim }\limits_{x \to - \infty } c =c\) (với \(c\) là hằng số).
+ \(\mathop {\lim }\limits_{x \to + \infty } \frac{1}{{{x^k}}} = 0\) với \(k \in \mathbb{N}^*\); \(\mathop {\lim }\limits_{x \to - \infty } \frac{1}{{{x^k}}} = 0\) với \(k \in \mathbb{N}^*\).
1.3. Giới hạn vô cực của hàm số tại một điểm
a) Giới hạn vô cực
|
Giả sử (a, b) là một khoảng chứa \(x_0\) và hàm số \(y = f(x)\) xác định trên khoảng (a, b)\(\backslash \{x_0\}\). - Ta nói hàm số \(y = f(x)\) có giới hạn \(+\infty\) khi \(x\to x_0\) nếu với dãy số (\(x_n\)) bất kì, \(x_n\in (a, b)\backslash \{x_0\}\) và \(x_n \to x_0\), ta có \(f(x_n) \to +\infty\). Kí hiệu: \(\lim \limits_{x \to {x_0} }f(x) = +\infty \) . - Ta nói hàm số \(y = f(x)\) có giới hạn \(-\infty\) khi \(x\to x_0\) nếu \(\lim \limits_{x \to {x_0} }[-f(x)] = +\infty \). Kí hiệu: \(\lim \limits_{x \to {x_0} }f(x) = -\infty \) . |
b) Một số quy tắc tính giới hạn vô cực
Chú ý: Các quy tắc tính giới hạn hữu hạn không còn đúng cho giới hạn vô cực.
Ta có một số quy tắc tính giới hạn của tích và thương hai hàm số khi một trong hai hàm số đó có giới hạn vô cực.
Quy tắc tìm giới hạn của tích f(x)g(x).
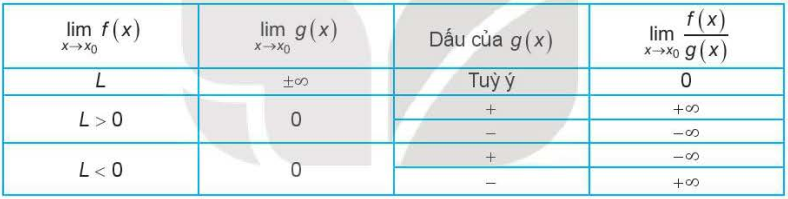
Quy tắc tìm giới hạn của thương \(\dfrac{{{f(x)}}}{{{g(x)}}}\).
Bài tập minh họa
Bài toán 1: Tìm \(\mathop {\lim }\limits_{x \to {x_0}} f(x)\) biết \(f(x)\) xác định tại \({x_0}\).
- Phương pháp:
+ Nếu \(f(x)\) là hàm số cho bởi một công thức thì giá trị giới hạn bằng \(f({x_0})\)
+ Nếu \(f(x)\) cho bởi nhiều công thức, khi đó ta sử dụng điều kiện để hàm số có giới hạn (Giới hạn trái bằng giới hạn phải).
Ví dụ 1: Tìm các giới hạn sau:
a) \(\mathop {\lim }\limits_{x \to 0} \frac{{\sin 2x + 3\cos x + x}}{{2x + {{\cos }^2}3x}}\)
b) \(\mathop {\lim }\limits_{x \to 2} \frac{{\sqrt {{x^2} + 3} - 2x}}{{\sqrt[3]{{x + 6}} + 2x - 1}}\)
Hướng dẫn giải
a) Ta có: \(\mathop {\lim }\limits_{x \to 0} \frac{{\sin 2x + 3\cos x + x}}{{2x + {{\cos }^2}3x}} = \frac{{\sin 0 + 3\cos 0 + 0}}{{2.0 + {{\cos }^2}0}} = 3\)
b) Ta có: \(\mathop {\lim }\limits_{x \to 2} \frac{{\sqrt {{x^2} + 3} - 2x}}{{\sqrt[3]{{x + 6}} + 2x - 1}} = \frac{{\sqrt {{2^2} + 3} - 2.2}}{{\sqrt[3]{{2 + 6}} + 2.2 - 1}} = \frac{{\sqrt 7 - 4}}{5}\).
Bài toán 2: Tìm \(A = \mathop {\lim }\limits_{x \to {x_0}} \frac{{f(x)}}{{g(x)}}\) trong đó \(f({x_0}) = g({x_0}) = 0\).
- Dạng này ta gọi là dạng vô định\(\frac{0}{0}\).
- Để khử dạng vô định này ta sử dụng phương pháp Hóc-ne cho đa thức.
Ví dụ 2: Tính các giới hạn sau:
a) Tìm giới hạn \(A = \mathop {\lim }\limits_{x \to 1} \frac{{{x^3} - 3{x^2} + 2}}{{{x^2} - 4x + 3}}.\)
b) Tìm giới hạn \(B = \mathop {\lim }\limits_{x \to 2} \frac{{{x^4} - 5{x^2} + 4}}{{{x^3} - 8}}.\)
Hướng dẫn giải
a) Ta có: \(A = \mathop {\lim }\limits_{x \to 1} \frac{{{x^3} - 3{x^2} + 2}}{{{x^2} - 4x + 3}} = \mathop {\lim }\limits_{x \to 1} \frac{{(x - 1)({x^2} - 2x - 2)}}{{(x - 1)(x - 3)}}\)\( = \mathop {\lim }\limits_{x \to 1} \frac{{{x^2} - 2x - 2}}{{x - 3}} = \frac{3}{2}\).
b) Ta có: \(B = \mathop {\lim }\limits_{x \to 2} \frac{{{x^4} - 5{x^2} + 4}}{{{x^3} - 8}} = \mathop {\lim }\limits_{x \to 2} \frac{{({x^2} - 1)({x^2} - 4)}}{{{x^3} - {2^3}}}\)\( = \mathop {\lim }\limits_{x \to 2} \frac{{({x^2} - 1)(x - 2)(x + 2)}}{{(x - 2)({x^2} + 2x + 4)}}\)\( = \mathop {\lim }\limits_{x \to 2} \frac{{({x^2} - 1)(x + 2)}}{{{x^2} + 2x + 4}} = 1\).
Luyện tập Bài 16 Toán 11 Kết Nối Tri Thức
Học xong bài học này, em có thể:
- Nhận biết khái niệm giới hạn hữu hạn của hàm số tại một điểm và tại vô cực, giới hạn một phía, giới hạn vô cực.
- Tính một số dạng giới hạn của hàm số. Giải quyết một số vấn đề thực tiễn gắn với giới hạn của hàm số.
3.1. Trắc nghiệm Bài 16 Toán 11 Kết Nối Tri Thức
Các em có thể hệ thống lại nội dung kiến thức đã học được thông qua bài kiểm tra Trắc nghiệm Toán 11 Kết nối tri thức Chương 5 Bài 16 cực hay có đáp án và lời giải chi tiết.
-
- A. \(2\).
- B. \(3\).
- C. \(-2\).
- D. \(+\infty \).
-
- A. \(-\frac{3}{2}\).
- B. \(0\).
- C. \(-2\).
- D. \(1\).
-
- A. \(a=11\), \(b=4\).
- B. \(a=11\), \(b=3\).
- C. \(a=10\), \(b=3\) .
- D. \(a=11\), \(b=5\).
Câu 4-10: Mời các em đăng nhập xem tiếp nội dung và thi thử Online để củng cố kiến thức về bài học này nhé!
3.2. Bài tập SGK Bài 16 Toán 11 Kết Nối Tri Thức
Các em có thể xem thêm phần hướng dẫn Giải bài tập Toán 11 Kết nối tri thức Chương 5 Bài 16 để giúp các em nắm vững bài học và các phương pháp giải bài tập.
Mở đầu trang 111 SGK Toán 11 Kết nối tri thức tập 1 - KNTT
Hoạt động 1 trang 111 SGK Toán 11 Kết nối tri thức tập 1 - KNTT
Luyện tập 1 trang 113 SGK Toán 11 Kết nối tri thức tập 1 - KNTT
Hoạt động 2 trang 113 SGK Toán 11 Kết nối tri thức tập 1 - KNTT
Luyện tập 2 trang 113 SGK Toán 11 Kết nối tri thức tập 1 - KNTT
Hoạt động 3 trang 114 SGK Toán 11 Kết nối tri thức tập 1 - KNTT
Luyện tập 3 trang 115 SGK Toán 11 Kết nối tri thức tập 1 - KNTT
Vận dụng trang 115 SGK Toán 11 Kết nối tri thức tập 1 - KNTT
Hoạt động 4 trang 115 SGK Toán 11 Kết nối tri thức tập 1 - KNTT
Hoạt động 5 trang 116 SGK Toán 11 Kết nối tri thức tập 1 - KNTT
Luyện tập 4 trang 116 SGK Toán 11 Kết nối tri thức tập 1 - KNTT
Luyện tập 5 trang 118 SGK Toán 11 Kết nối tri thức tập 1 - KNTT
Giải Bài 5.7 trang 118 SGK Toán 11 Kết nối tri thức tập 1 - KNTT
Giải Bài 5.8 trang 118 SGK Toán 11 Kết nối tri thức tập 1 - KNTT
Giải Bài 5.9 trang 118 SGK Toán 11 Kết nối tri thức tập 1 - KNTT
Giải Bài 5.10 trang 118 SGK Toán 11 Kết nối tri thức tập 1 - KNTT
Giải Bài 5.11 trang 118 SGK Toán 11 Kết nối tri thức tập 1 - KNTT
Giải Bài 5.12 trang 118 SGK Toán 11 Kết nối tri thức tập 1 - KNTT
Giải Bài 5.13 trang 118 SGK Toán 11 Kết nối tri thức tập 1 - KNTT
Bài tập 5.11 trang 83 SBT Toán 11 Tập 1 Kết nối tri thức - KNTT
Bài tập 5.12 trang 83 SBT Toán 11 Tập 1 Kết nối tri thức - KNTT
Bài tập 5.13 trang 83 SBT Toán 11 Tập 1 Kết nối tri thức - KNTT
Bài tập 5.14 trang 83 SBT Toán 11 Tập 1 Kết nối tri thức - KNTT
Bài tập 5.15 trang 83 SBT Toán 11 Tập 1 Kết nối tri thức - KNTT
Bài tập 5.16 trang 83 SBT Toán 11 Tập 1 Kết nối tri thức - KNTT
Bài tập 5.17 trang 83 SBT Toán 11 Tập 1 Kết nối tri thức - KNTT
Bài tập 5.18 trang 83 SBT Toán 11 Tập 1 Kết nối tri thức - KNTT
Bài tập 5.19 trang 83 SBT Toán 11 Tập 1 Kết nối tri thức - KNTT
Bài tập 5.20 trang 83 SBT Toán 11 Tập 1 Kết nối tri thức - KNTT
Hỏi đáp Bài 16 Toán 11 Kết Nối Tri Thức
Trong quá trình học tập nếu có thắc mắc hay cần trợ giúp gì thì các em hãy comment ở mục Hỏi đáp, Cộng đồng Toán học HOC247 sẽ hỗ trợ cho các em một cách nhanh chóng!
Chúc các em học tập tốt và luôn đạt thành tích cao trong học tập!
-- Mod Toán Học 11 HỌC247












