Phß║¦n hŲ░ß╗øng dß║½n giß║Żi b├Āi tß║Łp To├Īn 11 ChŲ░ŲĪng B├Āi 3 Cß║źp sß╗æ cß╗Öng sß║Į gi├║p c├Īc em nß║»m ─æŲ░ß╗Żc phŲ░ŲĪng ph├Īp v├Ā r├©n luyß╗ćn k─® n─āng c├Īc giß║Żi b├Āi tß║Łp tß╗½ SGK ─Éß║Īi sß╗æ v├Ā Giß║Żi t├Łch 11 CŲĪ bß║Żn-N├óng cao.
-
B├Āi tß║Łp 1 trang 97 SGK ─Éß║Īi sß╗æ & Giß║Żi t├Łch 11
Trong c├Īc d├Ży sß╗æ sau ─æ├óy, d├Ży sß╗æ n├Āo l├Ā cß║źp sß╗æ cß╗Öng? T├Łnh sß╗æ hß║Īng ─æß║¦u v├Ā c├┤ng sai cß╗¦a n├│:
a) \(u_n = 5 - 2n\);
b) \(u_n =\frac{n}{2}-1\);
c) \(u_n = 3^n\);
d) \(u_n =\frac{7-3n}{2}\)
-
B├Āi tß║Łp 2 trang 97 SGK ─Éß║Īi sß╗æ & Giß║Żi t├Łch 11
T├¼m sß╗æ hß║Īng ─æß║¦u v├Ā c├┤ng sai cß╗¦a c├Īc cß║źp sß╗æ cß╗Öng sau, biß║┐t:
a) \(\left\{\begin{matrix} u_{1}-u_{3}+u_{5}=10\\ u_{1}+u_{6=17} \end{matrix}\right.\)
b) \(\left\{\begin{matrix} u_{7}-u_{3}=8\\ u_{2}.u_{7}=75 \end{matrix}\right.\).
-
B├Āi tß║Łp 3 trang 97 SGK ─Éß║Īi sß╗æ & Giß║Żi t├Łch 11
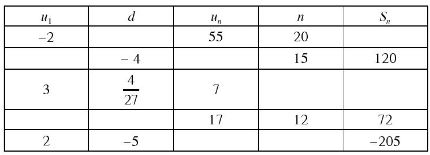
Trong c├Īc b├Āi to├Īn vß╗ü cß║źp sß╗æ cß╗Öng, ta thŲ░ß╗Øng gß║Ęp n─ām ─æß║Īi lŲ░ß╗Żng \(u_1, n, d, u_n, S_n.\)
a) H├Ży viß║┐t c├Īc hß╗ć thß╗®c li├¬n hß╗ć giß╗»a c├Īc ─æß║Īi lŲ░ß╗Żng ─æß╗ā c├│ thß╗ā t├¼m ─æŲ░ß╗Żc c├Īc ─æß║Īi lŲ░ß╗Żng c├▓n lß║Īi?
b) Lß║Łp bß║Żng theo mß║½u sau v├Ā ─æiß╗ün v├Āo chß╗Ś trß╗æng th├Łch hß╗Żp:
-
B├Āi tß║Łp 4 trang 98 SGK ─Éß║Īi sß╗æ & Giß║Żi t├Łch 11
Mß║Ęt s├Ān tß║¦ng mß╗Öt cß╗¦a mß╗Öt ng├┤i nh├Ā cao hŲĪn mß║Ęt s├ón 0,5 m. Cß║¦u thang ─æi tß╗½ tß║¦ng mß╗Öt l├¬n tß║¦ng 2 gß╗ōm 21 bß║Łc, mß╗Śi bß║Łc cao 18 cm.
a) H├Ży viß║┐t c├┤ng thß╗®c ─æß╗ā t├¼m ─æß╗Ö cao cß╗¦a mß╗Öt bß║Łc tuß╗│ ├Į so vß╗øi mß║Ęt s├ón.
b) T├Łnh ─æß╗Ö cao cß╗¦a s├Ān tß║¦ng hai so vß╗øi mß║Ęt s├ón.
-
B├Āi tß║Łp 5 trang 98 SGK ─Éß║Īi sß╗æ & Giß║Żi t├Łch 11
Tß╗½ giß╗Ø ─æß║┐n 12 giß╗Ø trŲ░a, ─æß╗ōng hß╗ō ─æ├Īnh bao nhi├¬u tiß║┐ng, nß║┐u n├│ chß╗ē ─æ├Īnh chu├┤ng b├Īo giß╗Ø v├Ā sß╗æ tiß║┐ng chu├┤ng bß║▒ng sß╗æ giß╗Ø
-
B├Āi tß║Łp 3.18 trang 123 SBT To├Īn 11
Cho d├Ży sß╗æ (un) vß╗øi un = 1 - 7n
a) Khß║Żo s├Īt t├Łnh t─āng, giß║Żm cß╗¦a d├Ży sß╗æ ;
b) Chß╗®ng minh d├Ży sß╗æ tr├¬n l├Ā cß║źp sß╗æ cß╗Öng. Lß║Łp c├┤ng thß╗®c truy hß╗ōi cß╗¦a d├Ży sß╗æ ;
c) T├Łnh tß╗Ģng 100 sß╗æ hß║Īng ─æß║¦u cß╗¦a d├Ży sß╗æ.
-
B├Āi tß║Łp 3.19 trang 124 SBT To├Īn 11
Trong c├Īc d├Ży sß╗æ (un) sau ─æ├óy, d├Ży sß╗æ n├Āo l├Ā cß║źp sß╗æ cß╗Öng?
a) un = 3n ŌłÆ 1;
b) un = 2n + 1;
c) un = (n+1)2 ŌłÆ n2;
d) \(\left\{ \begin{array}{l}
{u_1} = 3\\
{u_{n + 1}} = 1 - {u_n}
\end{array} \right.\) -
B├Āi tß║Łp 3.20 trang 124 SBT To├Īn 11
T├Łnh sß╗æ hß║Īng ─æß║¦u u1 v├Ā c├┤ng sai d cß╗¦a cß║źp sß╗æ cß╗Öng (un) biß║┐t :
a) \(\left\{ \begin{array}{l}
{u_1} + 2{u_5} = 0\\
{S_4} = 14
\end{array} \right.\)b) \(\left\{ \begin{array}{l}
{u_4} = 10\\
{u_7} = 19
\end{array} \right.\)c) \(\left\{ \begin{array}{l}
{u_1} + {u_5} - {u_3} = 10\\
{u_1} + {u_6} = 7
\end{array} \right.\)d) \(\left\{ \begin{array}{l}
{u_7} - {u_3} = 8\\
{u_2}.{u_1} = 75
\end{array} \right.\) -
B├Āi tß║Łp 3.21 trang 124 SBT To├Īn 11
T├Łnh sß╗æ c├Īc sß╗æ hß║Īng cß╗¦a cß║źp sß╗æ cß╗Öng (an), nß║┐u
\(\left\{ \begin{array}{l}
{a_2} + {a_4} + ... + {a_{2n}} = 126\\
{a_2} + {a_{2n}} = 42
\end{array} \right.\) -
B├Āi tß║Łp 3.22 trang 124 SBT To├Īn 11
T├¼m cß║źp sß╗æ cß╗Öng (un) biß║┐t
a) \(\left\{ \begin{array}{l}
{u_1} + {u_2} + {u_3} = 27\\
u_1^2 + u_2^2 + u_3^2 = 275
\end{array} \right.\)b) \(\left\{ \begin{array}{l}
{u_1} + {u_2} + ... + {u_n} = a\\
u_1^2 + u_2^2 + ... + u_n^2 = {b^2}
\end{array} \right.\) -
B├Āi tß║Łp 3.23 trang 124 SBT To├Īn 11
T├¼m x tß╗½ phŲ░ŲĪng tr├¼nh
a) 2 + 7 + 12 + ... + x = 245, biß║┐t 2, 7, 12, ..., x l├Ā cß║źp sß╗æ cß╗Öng.
b) (2x + 1) + (2x + 6) + (2x + 11) + ... + (2x + 96) = 1010 biß║┐t 1, 6, 11, ... l├Ā cß║źp sß╗æ cß╗Öng.
-
B├Āi tß║Łp 3.24 trang 124 SBT To├Īn 11
H├Ży chß╗Źn cß║źp sß╗æ cß╗Öng trong c├Īc d├Ży sß╗æ (un) sau:
A. \({u_n} = {2^n} + 1\)
B. \({u_n} = \frac{{{3^n}}}{n}\)
C. \(u_n=5n\)
D. \(\left\{ \begin{array}{l}
{u_1} = 1\\
{u_{n + 1}} = {u_n} + n,\,\,n \ge 1
\end{array} \right.\) -
B├Āi tß║Łp 3.25 trang 124 SBT To├Īn 11
Cho cß║źp sß╗æ cß╗Öng u1 = -2; u19 = 52. Tß╗Ģng cß╗¦a 20 sß╗æ hß║Īng ─æß║¦u l├Ā:
A. 1060 B. -570 C. 530 D. -530
-
B├Āi tß║Łp 3.26 trang 124 SBT To├Īn 11
Cho cß║źp sß╗æ cß╗Öng 5, x, y, 17. Khi ─æ├│:
A. x = 9; y = 12 B. x = 8; y = 14
C. x = 7; y = 12 D. x = 9; y = 13
-
B├Āi tß║Łp 19 trang 114 SGK To├Īn 11 NC
Chß╗®ng minh rß║▒ng mß╗Śi d├Ży sß╗æ sau l├Ā mß╗Öt cß║źp sß╗æ cß╗Öng v├Ā h├Ży x├Īc ─æß╗ŗnh c├┤ng sai cß╗¦a cß║źp sß╗æ cß╗Öng ─æ├│:
a. D├Ży sß╗æ (un) vß╗øi un = 19nŌĆō5;
b. D├Ży sß╗æ (un) vß╗øi un = an+b, trong ─æ├│ a v├Ā b l├Ā c├Īc hß║▒ng sß╗æ.
-
B├Āi tß║Łp 20 trang 114 SGK To├Īn 11 NC
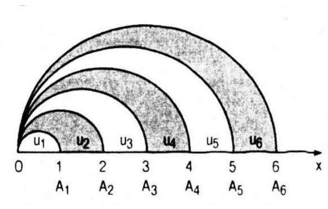
Tr├¬n tia Ox lß║źy ├Īc ─æiß╗ām A1, A2, ŌĆ”, An,ŌĆ” sao cho mß╗Śi sß╗æ nguy├¬n dŲ░ŲĪng n, OAn = n. Trong c├╣ng mß╗Öt nß╗Ła mß║Ęt phß║│ng c├│ bß╗Ø l├Ā ─æŲ░ß╗Øng thß║│ng chß╗®a tia Ox, vß║Į c├Īc nß╗Ła ─æŲ░ß╗Øng tr├▓n ─æŲ░ß╗Øng k├Łnh OAn, n= 1,2,ŌĆ” K├Ł hiß╗ću l├Ā diß╗ćn t├Łch cß╗¦a nß╗Ła h├¼nh tr├▓n ─æŲ░ß╗Øng k├Łnh OA1 v├Ā vß╗øi mß╗Śi n Ōēź 2, k├Ł hiß╗ću un l├Ā diß╗ćn t├Łch cß╗¦a h├¼nh giß╗øi hß║Īn bß╗¤i nß╗Ła ─æŲ░ß╗Øng tr├▓n ─æŲ░ß╗Øng k├Łnh OAn -1 , nß╗Ła ─æŲ░ß╗Øng tr├▓n ─æŲ░ß╗Øng k├Łnh OAn v├Ā tia Ox. Chß╗®ng minh rß║▒ng d├Ży sß╗æ (un) l├Ā mß╗Öt cß║źp sß╗æ cß╗Öng. H├Ży x├Īc ─æß╗ŗnh c├┤ng sai cß╗¦a cß║źp sß╗æ cß╗Öng ─æ├│.
-
B├Āi tß║Łp 21 trang 114 SGK To├Īn 11 NC
Trong mß╗Śi c├óu sau, h├Ży ─æ├Īnh dß║źu ŌĆ£xŌĆØ v├Āo phß║¦n kß║┐t luß║Łn m├Ā em cho l├Ā ─æ├║ng :
a. Mß╗Śi cß║źp sß╗æ cß╗Öng vß╗øi c├┤ng sai d>0d>0 l├Ā mß╗Öt d├Ży sß╗æ
 T─āng
T─āng Giß║Żm
Giß║Żm Kh├┤ng t─āng c┼®ng kh├┤ng giß║Żm.
Kh├┤ng t─āng c┼®ng kh├┤ng giß║Żm.b. Mß╗Śi cß║źp sß╗æ cß╗Öng vß╗øi c├┤ng sai d<0d<0 l├Ā mß╗Öt d├Ży sß╗æ
 T─āng
T─āng Giß║Żm
Giß║Żm Kh├┤ng t─āng c┼®ng kh├┤ng giß║Żm.
Kh├┤ng t─āng c┼®ng kh├┤ng giß║Żm. -
B├Āi tß║Łp 22 trang 115 SGK To├Īn 11 NC
Mß╗Öt cß║źp sß╗æ cß╗Öng c├│ n─ām sß╗æ hß║Īng m├Ā tß╗Ģng cß╗¦a sß╗æ hß║Īng ─æß║¦u v├Ā sß╗æ hß║Īng thß╗® ba bß║▒ng 28, tß╗Ģng cß╗¦a sß╗æ hß║Īng thß╗® ba v├Ā sß╗æ hß║Īng cuß╗æi bß║▒ng 40. H├Ży t├¼m cß║źp sß╗æ cß╗Öng ─æ├│.
-
B├Āi tß║Łp 23 trang 115 SGK To├Īn 11 NC
Cho cß║źp sß╗æ cß╗Öng (un) c├│ u20 = ŌłÆ 52 v├Ā u51 = ŌłÆ 145. H├Ży t├¼m sß╗æ hß║Īng tß╗Ģng qu├Īt cß╗¦a cß║źp sß╗æ cß╗Öng ─æ├│.
-
B├Āi tß║Łp 24 trang 115 SGK To├Īn 11 NC
Cho cß║źp sß╗æ cß╗Öng (un) vß╗øi c├┤ng sai d v├Ā cho c├Īc sß╗æ nguy├¬n dŲ░ŲĪng m v├Ā k, vß╗øi m Ōēź k. Chß╗®ng minh rß║▒ng um = uk+(mŌłÆk)d.
├üp dß╗źng: H├Ży t├¼m c├┤ng sai d cß╗¦a cß║źp sß╗æ cß╗Öng (un) m├Ā u18 ŌłÆ u3 = 75.
-
B├Āi tß║Łp 25 trang 115 SGK To├Īn 11 NC
Cho cß║źp sß╗æ cß╗Öng (un) c├│ u1ŌłÆu3 = 6 v├Ā u5 = ŌłÆ10. H├Ży t├¼m c├┤ng sai v├Ā sß╗æ hß║Īng tß╗Ģng qu├Īt cß╗¦a cß║źp sß╗æ cß╗Öng ─æ├│.
-
B├Āi tß║Łp 26 trang 115 SGK To├Īn 11 NC
H├Ży chß╗®ng minh ─æß╗ŗnh l├Ł 3.
-
B├Āi tß║Łp 27 trang 115 SGK To├Īn 11 NC
Cho cß║źp sß╗æ cß╗Öng (un) c├│ u2+u22 = 60. H├Ży t├Łnh tß╗Ģng 23 sß╗æ hß║Īng ─æß║¦u ti├¬n cß╗¦a cß║źp sß╗æ cß╗Öng ─æ├│.
-
B├Āi tß║Łp 28 trang 116 SGK To├Īn 11 NC
Sß╗æ ─æo ba g├│c cß╗¦a mß╗Öt tam gi├Īc vu├┤ng lß║Łp th├Ānh mß╗Öt cß║źp sß╗æ cß╗Öng. H├Ży t├¼m sß╗æ ─æo ba g├│c ─æ├│.